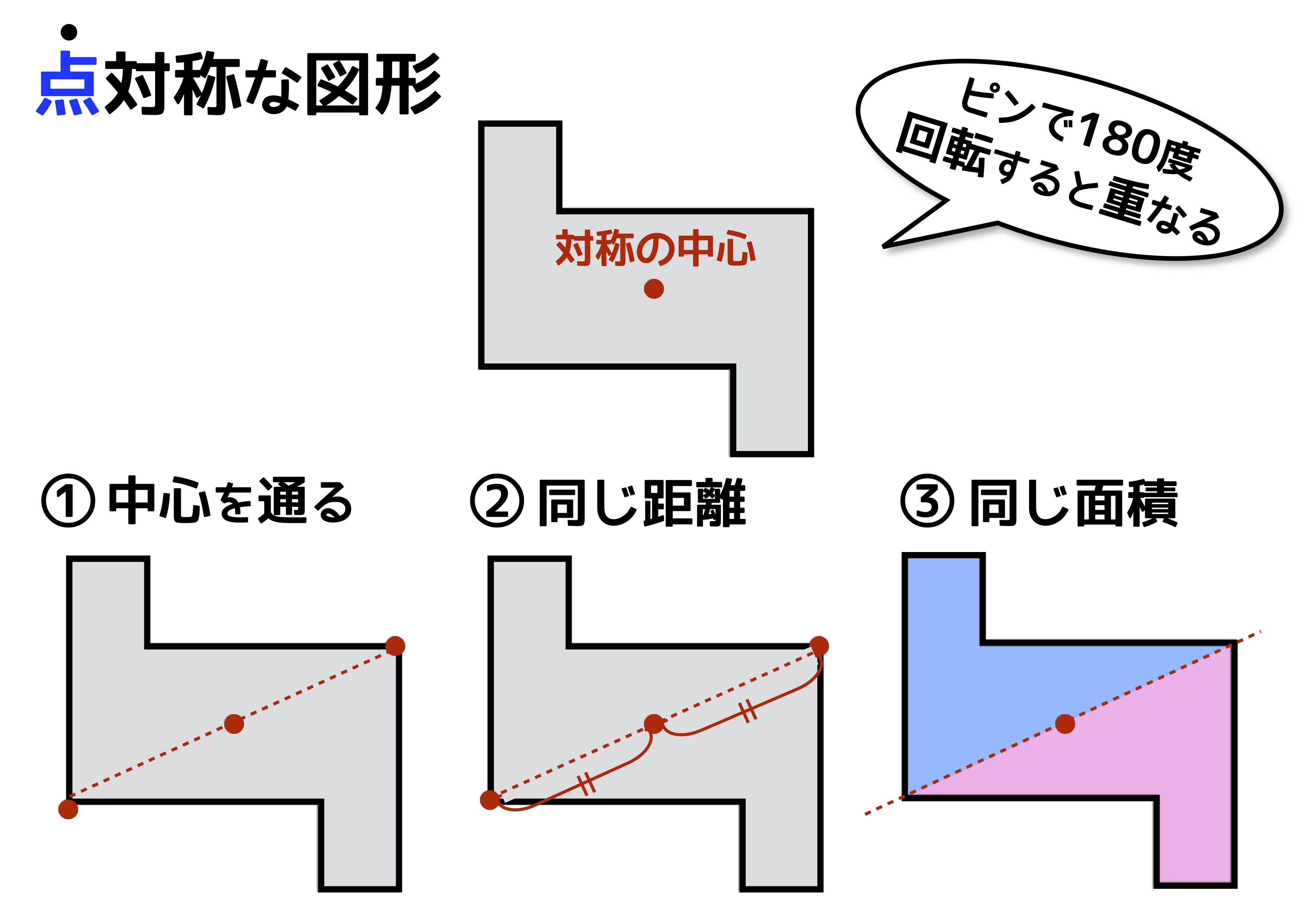
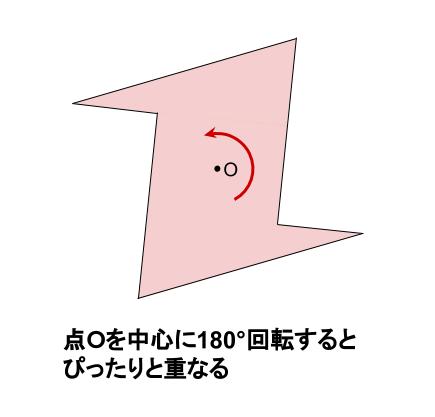
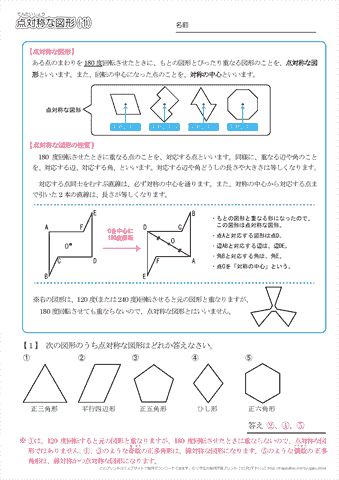
次の図のように,ある点を中心に180°回転させたとき,元の図形と一致する図形を 点対称な図形 といいます。 このとき回転の中心となる点を 対称の中心 といいます。 右の図は平行四辺形が対角線の交点を対称の中心とする点対称な図形であることを示しています。 点対称な図形では,次の図のように1つの点から対称の中心を突き抜けて向こう側に同じ距離だけ線対称な図形には対称軸が必ず \(\boldsymbol{1}\) 本あり、複数の対称軸を持つ図形もあります。ある点を中心として\(180^{\circ}\) 回転すると、もとの図形にぴったり重なり合う状態を 点対称(てんたいしょう)であるといい、そのような図形を 点対称な図形 と技能 線対称、点対称な図形をかくことができる。 知識・理解 線対称、点対称な図形の意味や性質について理解する。 時 学習活動 研究上の手立て 間 ①自分 の内面 とつながり②友達 ③既習事項 1

スマホok 6年 対称な図形 多角形と対称 Youtube
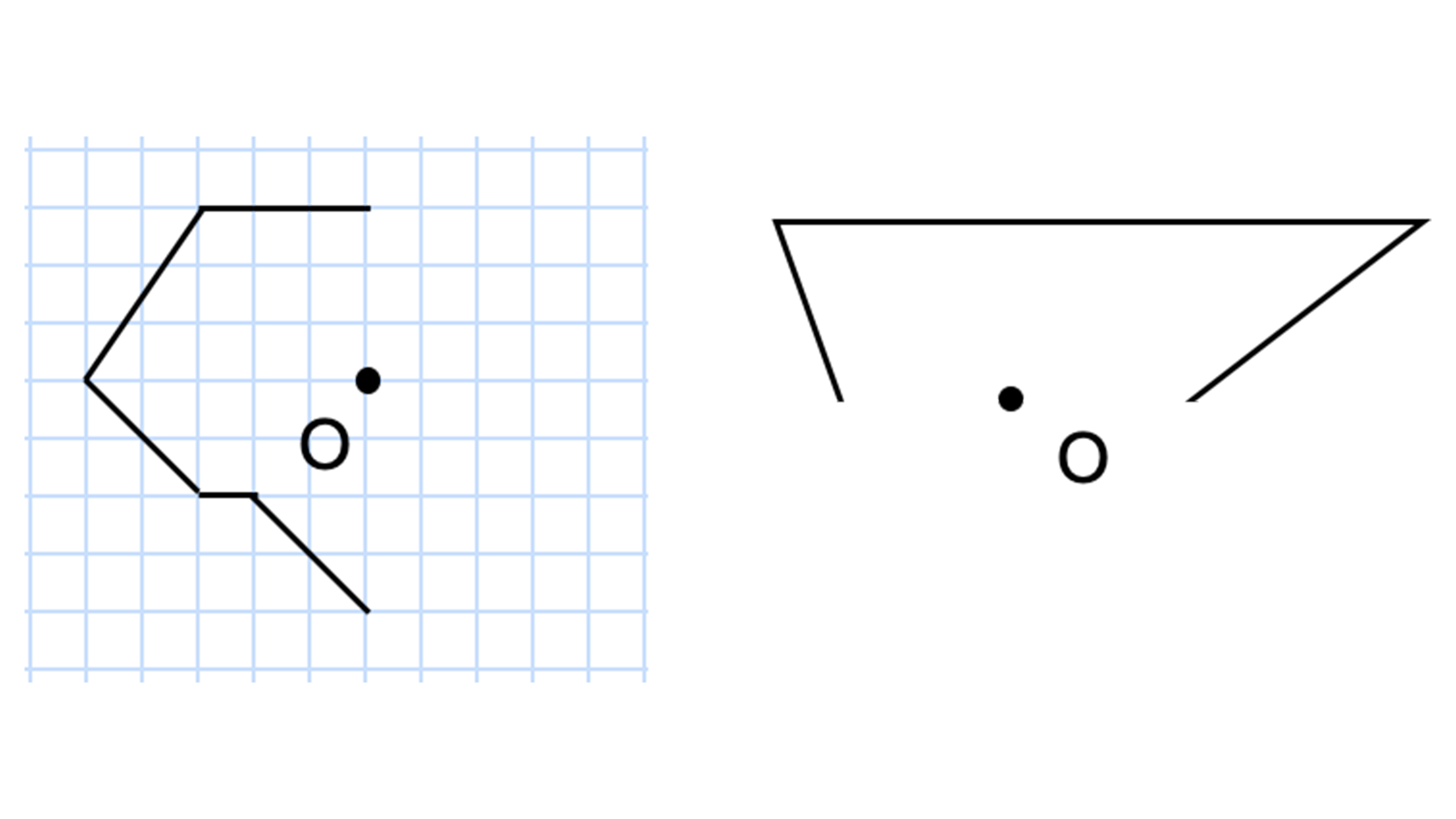
点対称な図形 複雑
点対称な図形 複雑- 平面図形というと、小学生がつまずきやすいポイントとして、・ 複雑な形の面積・ 角度・ 線対称・点対称があげられます。このうち「線対称・点対称」は、図形問題全体に対する基礎力を養うのに格好の題材です。線対称は、鏡やガラスなど、身近なものを使えば、比較的簡単にイメージすることができますが、点描写することによって、左右が対称である複雑な図形でも左右対称図形であれば,処理すべき情報は対称軸を境に左右いずれかの半分 ですむ.対称性構造は知覚的複雑さを大きく低下させ,図形のよさを高める最重要なパター ンとなる(例えばYodogawa(19) など). 対称性を中心とした規則性の高い形は,対象を知覚するうえでの枠組み




世界一分かりやすい算数 小6 対称な図形
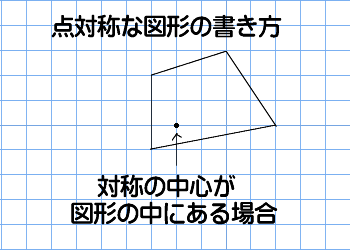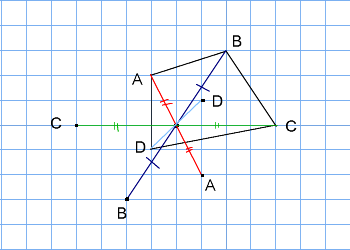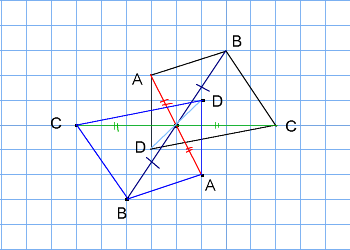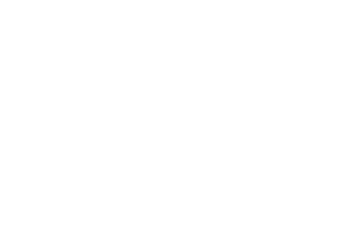
6年 点対称な図形|算数イメージ動画集|大日本図書 文部科学省『教育用コンテンツ開発事業』 プロペラは1つの点を中心として 180° 回転させるともとの図形に重なるため,点対称な図形といえます。 点対称な図形では,対応する点を結ぶ線分は対称の点対称な図形の書き方に慣れましょう。 点対称な図形の書き方その3 対称の中心が図形の中にある場合は 下の動画のように書きます ↓ 動画作成協力・・動くイラストフリー素材 教え方3 線対称や点対称の考え方をもとにして、正多角形と対称な図形の見方に気づかせます。 この続きは次の点対称移動(回転の中心を動かす) 点対称移動(回転の中心を動かす) 複雑な図形の面積 ;
知点対称な図形,対称の中心の意 味を理解している。 対応する点,辺,角の意 味について理解する。 点対称な図形について,重なり合う頂 点,辺,角を調べる。 対応する点,辺,角の意味を知る。 対応する辺の長さや角の大きさを比 べる。#数学 #算数 心得・活用のポイント 算数・数学は答えが1つですが、様々に思考を巡らし解に到達する必要があります。 その過程で、シンキングツールを使って『思考を可視化』することにより,思考が深まることができます。 黄金パターン 例えば、具体的な事柄から一般的な事柄を導く、様々小学6年生の算数 点対称な図形 問題プリント 小学6年生の算数点対称な図形 問題プリントを無料ダウンロード・印刷 (プリント5枚) 小学6年生の算数 円の面積 問題プリント 小学6年生の算数円の面積の問題プリントを無料ダウンロード・印刷 (プリント6枚) 小学6年生の算数 角柱
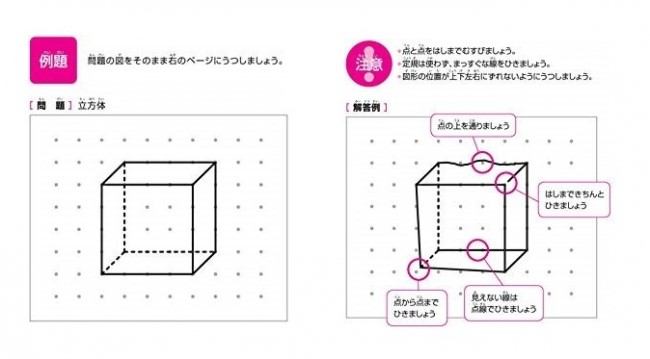
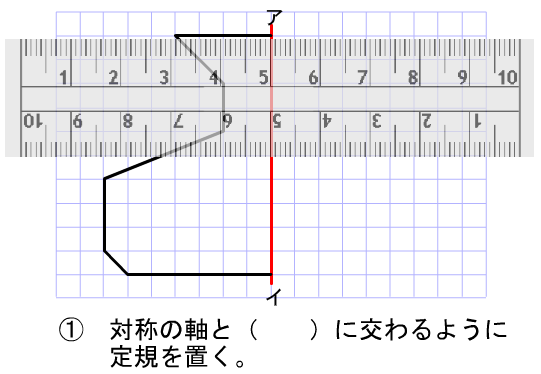
身の回りから線対称な図形を見つける。 T 線対称な形を見つけましょう。 教材の中には,基本図形だけでなく,身の回りの記号やアルファベットなど入れておく。また,点対称な図形も入れておき,折り曲げる操作ではぴったり重ならないことにも気づかせていきたい。 5 学習のまとめをする。 株式会社ディスカヴァー・トゥエンティワンのプレスリリース(年10月11日 12時10分) 10万部突破 小学生が一番苦手な立体図形はベストセラー宿題プリントの点対称な図形の書き方を紹介します。宿題をやるときの ヒントにしたり、やり方を確認したりしてみてね☆ 対称な図形をかくときは、 対応する頂点を見つけると カンタンにかくことができるよ! ① 頂点から、点O(中心)を通る直線を少し長めに引く 後で、この直線上に点を



線対称との違いは 点対称 な図形を理解しよう お役立ち情報ページ 個別指導の学習塾なら個別指導塾スタンダード



10万部突破 小学生が一番苦手な立体図形はベストセラードリルで克服しよう 株式会社ディスカヴァー トゥエンティワンのプレスリリース
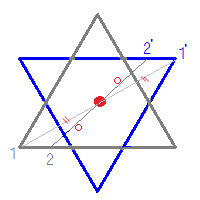
平面図形というと、小学生がつまずきやすいポイントとして、 ・ 複雑な形の面積 ・ 角度 ・ 線対称・点対称 があげられます。 このうち「線対称・点対称」は、図形問題全体に対する基礎力を養うのに格好の題材です。線対称は、鏡やガラスなど、身近なものを使えば、比較的簡単にイメージすることができますが、点描写することによって、左右が対称であるとグリッド点つなぎプリント 見本を見ながらグリッドに合わせて同じ図形を書く練習です。 運筆練習と一緒に空間認識、位置記憶力が鍛えられるプリントです。 ちなみに難易度「難しい」は小学校入試レベルなので幼児にとってはかなり難問です。 子供正方形は点対称な図形である. 例えば,正方形上の点1から中心までの距離 " を中心の反対側に伸ばした点 1' は元の正方形の上にあり,点2から中心までの距離 o を中心の反対側に伸ばした点 2' も元の正方形の上にある. このように,元の正方形(灰色)を180°回転すると元の図形と一致する. だから,正方形は点対称な図形である. 例3 正五角形は



線対称との違いは 点対称 な図形を理解しよう お役立ち情報ページ 個別指導の学習塾なら個別指導塾スタンダード



線対称と点対称 3つの性質を上手に使えるかどうかで得点に大きな差が出る 中学受験ナビ
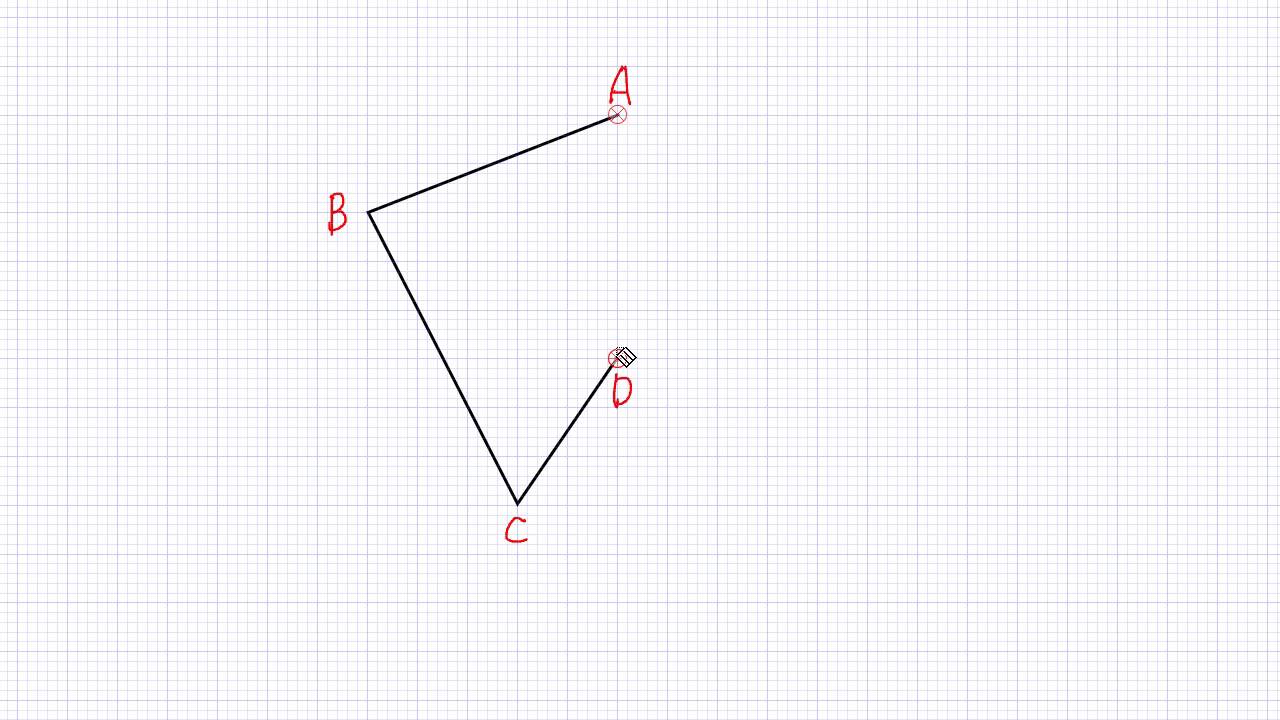
このようにどこかで折り曲げたら図形がピッタリ重なる線が引ける図形が、線対称の図形です。 また、線対称や点対称において重なることを 「対応」 と言い、重なる点や線を「対応する点」や「対応する線」と言います。図の正五角形の場合、「点b」と対応する点は「点e」、「辺de」と対応する辺は「辺cb」です。平面図形というと、小学生がつまずきやすいポイントとして、 ・ 複雑な形の面積 ・ 角度 ・ 線対称・点対称 があげられます。 このうち「線対称・点対称」は、図形問題全体に対する基礎力を養うのに格好の題材です。線対称は、鏡やガラスなど、身近な動くミニビースト sinの図形的意味 のコピー ;



線対称 点対称



Tossランド 線対称な図形 作図
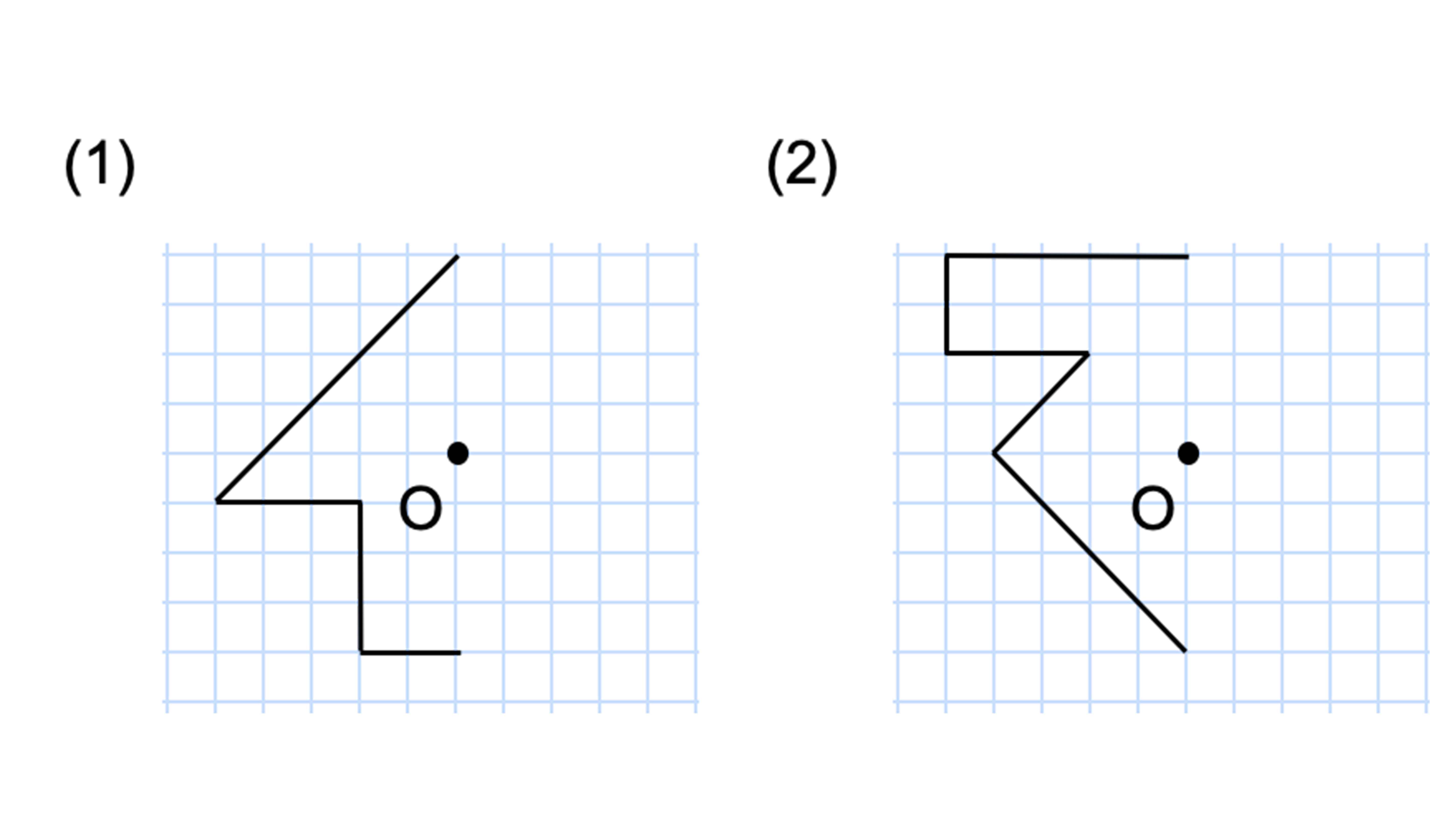
小6算数1学期 4月1対称な図形② なまえ 6 右の図は点対称な形である。直線ALと直線DIの交 わる点が,この形の( )である。 また,直線BOの長さが9cmのとき直線BKの長さは ( )cmである。 7 下の図で,線対称な形は( ),点対称な形は( ) である。 一番使いやすい(対称性がよい)とり方をするのが普通である。 もう少し複雑な例(現実の物質に近い例)を以下に示す。今まで単純化してきたこととして、格子点に原子があ ログイン 新規登録 『物性物理学1』§2:物質の構造 yukishiomi 『物性物理学1』§2:物質の構造 3 yukishiomi 年4月1日線対称 な図形 と点対称 な図形 の意味 や特徴 を比較 して 理解 する 活動 が不足 して いたことが 考えら れる 。 ・平成 21 年度 のB1(2)の結果 を見てみると 、正答率 が50 %である 。またこの 問題 は、無答率 が 19%と他の問題 と比べて 高くなって おり 、図形 の性質 や特徴 を的確 に




世界一分かりやすい算数 小6 対称な図形



中学数学 点対称な図形 中学数学の無料オンライン学習サイトchu Su
平面図形というと、小学生がつまずきやすいポイントとして、 ・ 複雑な形の面積 ・ 角度 ・ 線対称・点対称 があげられます。 このうち「線対称・点対称」は、図形問題全体に対する基礎力を養うのに格線対称な図形の性質は,次のようにまとめています。 点対称の定義 対称の中心のまわりに180°まわして重なる点,線,角をそれぞれ,対応する点,対応する線,対応する角といいます。 点対称な図形の性質は,次のようにまとめています。 線対称や点対称の図形を指導するには,実際に折ったりまわしたりして確かめることや,方眼紙や白紙に作図させて理解させる点対称な図形の代表例は平行四辺形です。 平行四辺形は点対称であり、線対称でない図形です。 長方形、ひし形、正方形はすべて平行四辺形なので、 点対称です。 ※かつ、線対称な図形でもあります。 平行四辺形以外で、 「点対称であり、線対称でない」図形は、




Motoo Tange S Blog 対称性の数学




世界一分かりやすい算数 小6 対称な図形
・線対称,点対称な形の作図 ・対称性に着目した基本図形の 考察 拡大図と縮図 ・拡大図の概念と性質 ・拡大図・縮図の作図 ・縮図の利用 2 きるといった経験をしてきている。 ②本学年での指導内容と留意点 学習指導要領には,5 学年の合同の内容について以下のように書かれている。 第考える力を育てる 天才ドリル 平面図形が得意になる点描写 線対称小学校全学年用 算数 認知工学 本の購入は楽天ブックスで。全品送料無料!購入毎に「楽天ポイント」が貯まってお得!みんなのレビュー・感想も満載。剿激図形: 図形それ自体がもっ 対称軸の種類により以 下の3条件に分けた。条件ユ: 線対称図形、条件2: 点対称図形、条件3: 対称性なし図形。い ずれの 図形 もマ ーカーとなる部分 ; 髑 をひとつ 設けてい る 。 条件1 図i ff 条件2 標準刺激の 図形 条件3



線対称 点対称 昇英塾




点対称 Wikipedia
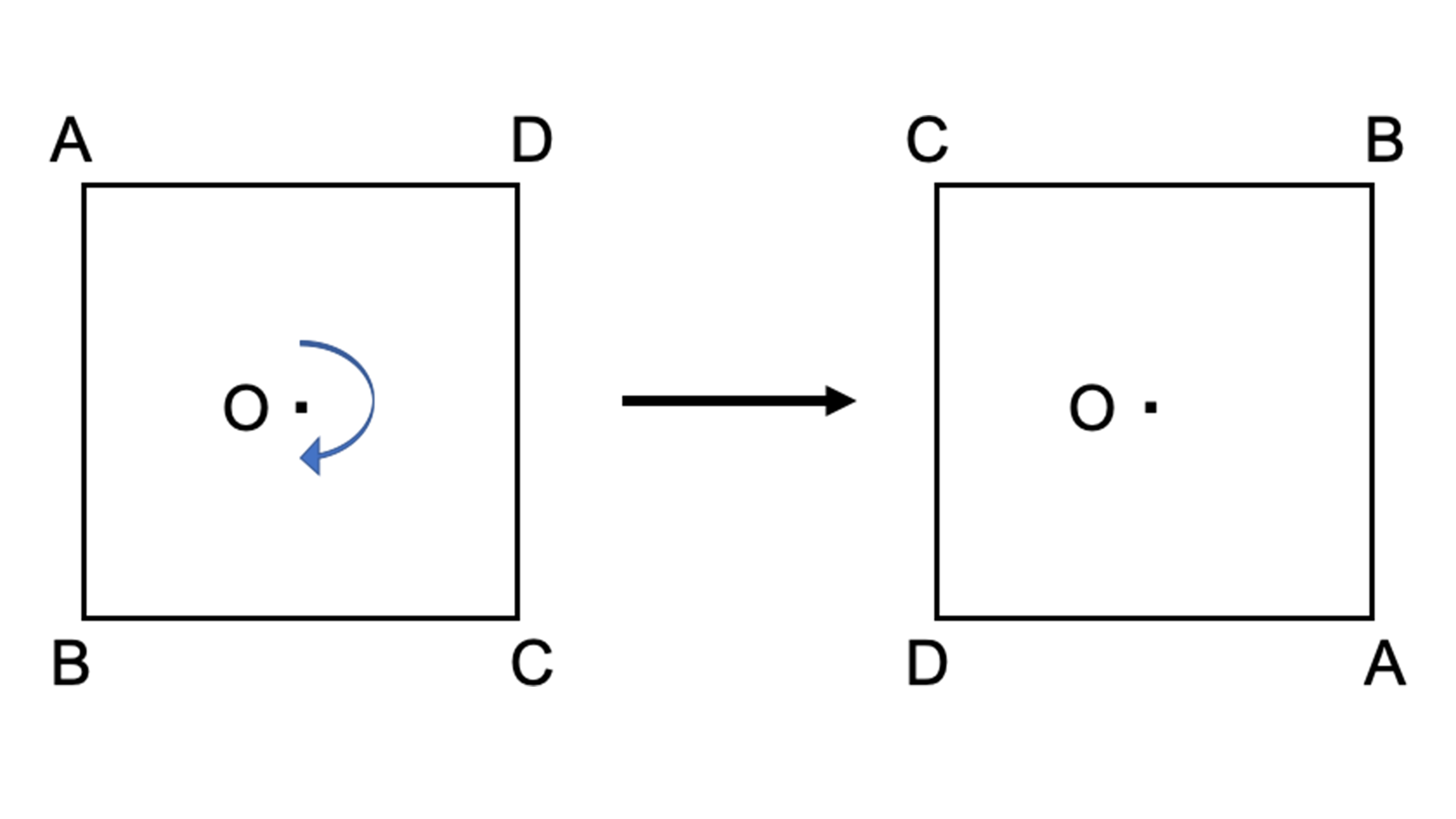
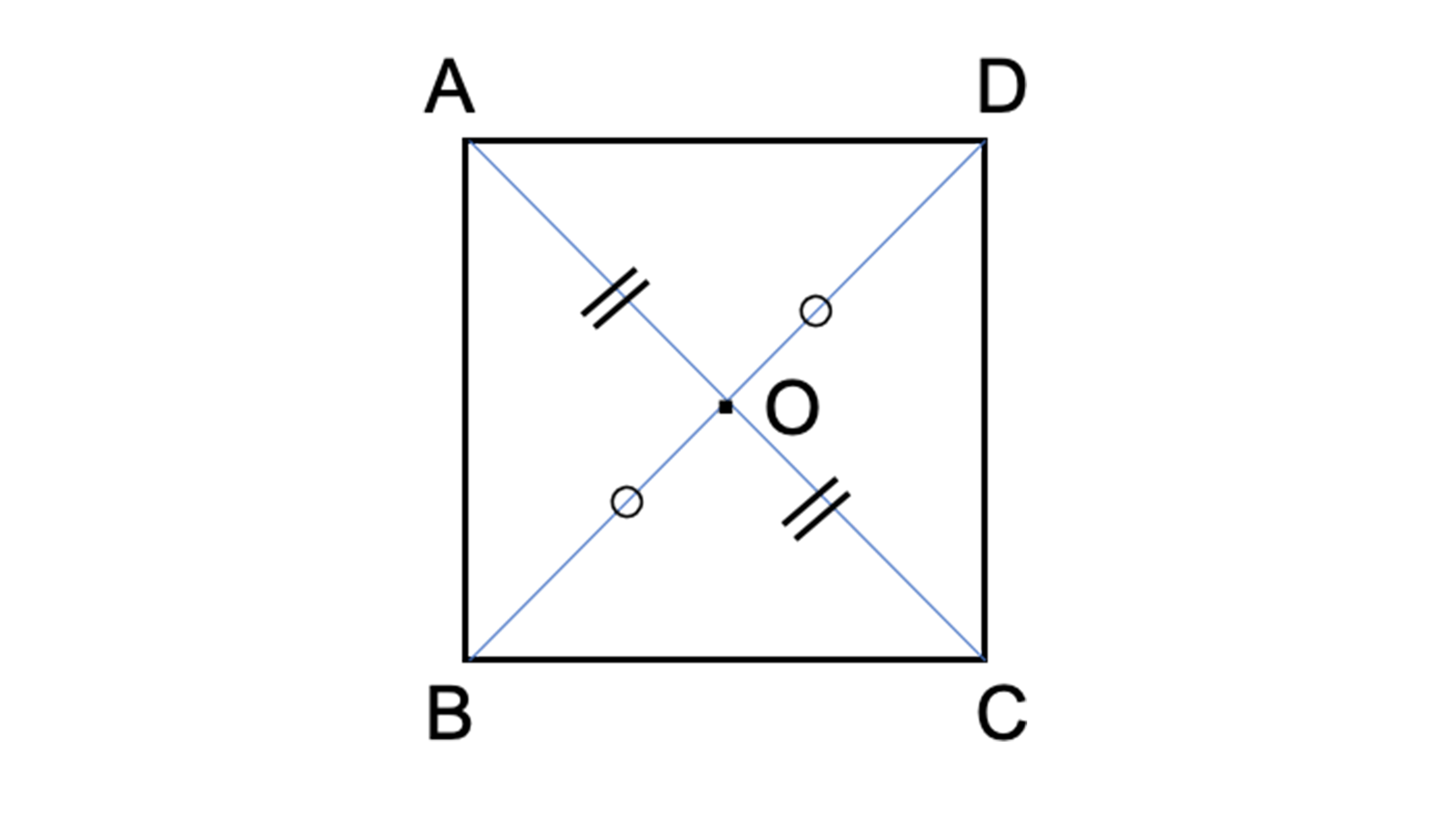
ブリタニカ国際大百科事典 小項目事典 点対称の用語解説 空間の1点oがある。oを通る線分上の2点p,qがoを中心として対応する位置にあるとき,この2点は点oに対して点対称であるという。また,1つの図形が,oに関する2直角の回転移動によって自分自身に重ね合せられるとき,この図形は点 「線対称な図形」というとなんだかむずかしく感じますが、遊びの延長線上で自然に「線対称な図形」に親しむことができます。 ぜひおうちでも取り組んでみてくださいね。 datamatchedcontentuitype="image_card_sidebyside" あわせて読みたい記事 おうち知育のヒントかたち 「図形が苦手」な子ども 先ほどの説明でも使った正方形ABCDを使って説明してみましょう。 正方形ABCDは原点Oを中心とした点対称の図形のため、対角線を引くと対応する点同士 (AとC、BとD)が結べました。 点対称の性質をアルファベットなどで示すと下のようになります。 このように対応する点同士を結び合わせて関係性を考えてみましょう。 ・ACとBDが



線対称との違いは 点対称 な図形を理解しよう お役立ち情報ページ 個別指導の学習塾なら個別指導塾スタンダード
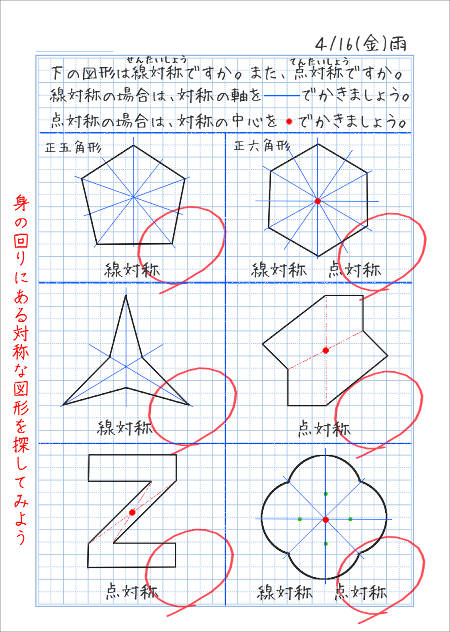



線対称と点対称の自主学習ノート 家庭学習レシピ
線対称・点対称の定義と違い|簡単な見分け方を解説 管理人 10月 6, 18 / 12月 4, 19 小学校算数の平面図形において『線対称』や『点対称』について習いますが、これらは他の単元とは少し毛並みが異なり、独特の思考が必要に 対称な図形 線対称基本1 無料で使える学習ドリル https//manabixsrvjp 2.対称図形の寸法表示 本連載・初級編の「形状の一部を省略して図面を描く(図形を省略できる場合の表示法)」で説明した内容に関連する事項ですが、対称図形の片側を省略する場合は、寸法線は中心線を超えた適宜の位置まで伸ばし、図を省略した側には矢印をつけません。 多数の直
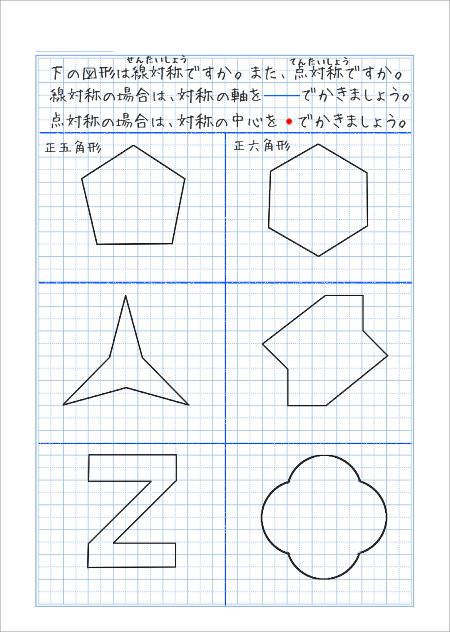



線対称と点対称の自主学習ノート 家庭学習レシピ
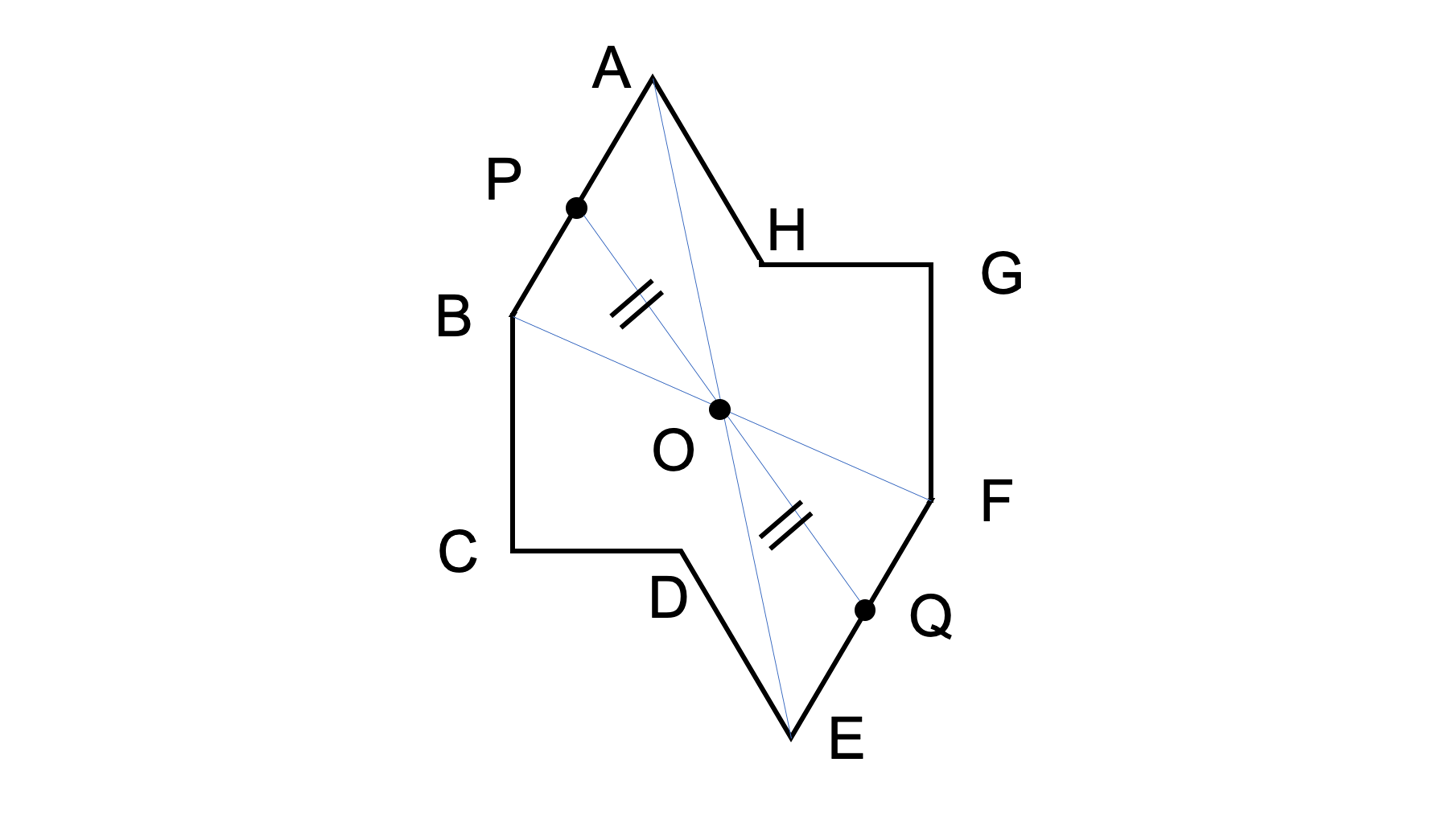



線対称との違いは 点対称 な図形を理解しよう お役立ち情報ページ 個別指導の学習塾なら個別指導塾スタンダード
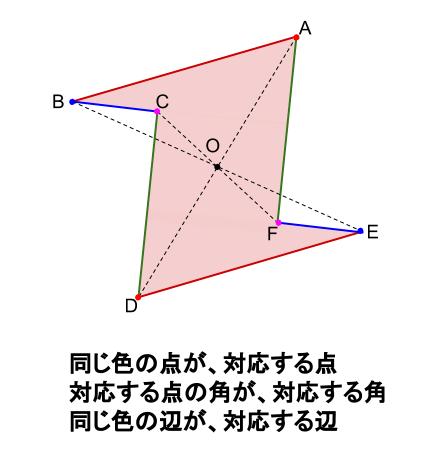



中学数学 点対称な図形 中学数学の無料オンライン学習サイトchu Su



点対称な図形




スマホok 6年 対称な図形 多角形と対称 Youtube
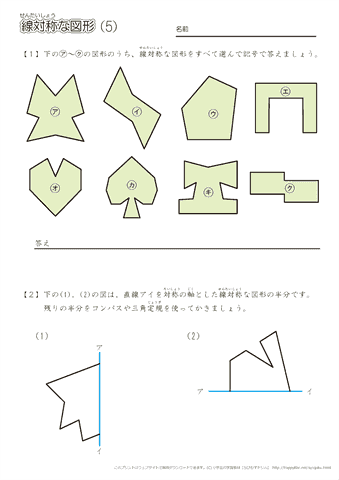



小学6年生の算数 線対称な図形 問題プリント ちびむすドリル 小学生



Http Www Otsu Ed Jp Kara E Topics6 Upl 21 1 Pdf




世界一分かりやすい算数 小6 対称な図形
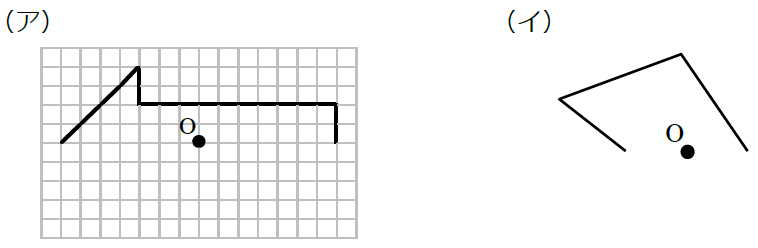



中1数学 点対称な図形とは まなビタミン
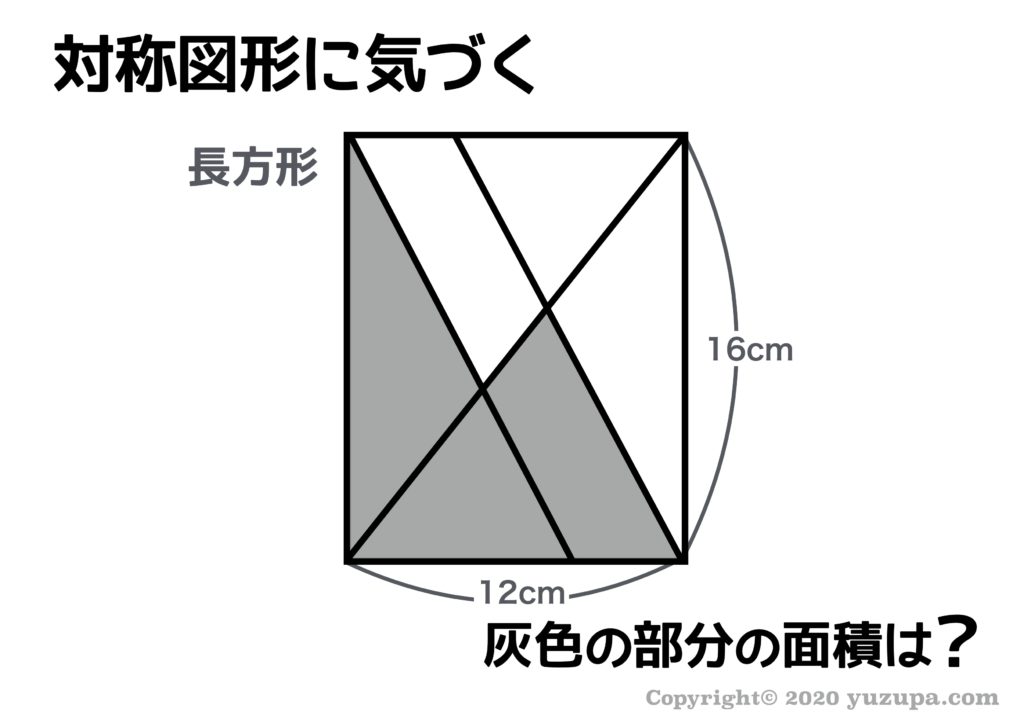



中学受験 図形の面積問題は 7つ道具 で攻略 かるび勉強部屋



点対称な図形のかき方 Youtube



線対称図形と点対称図形の見分け方 算数解法の極意
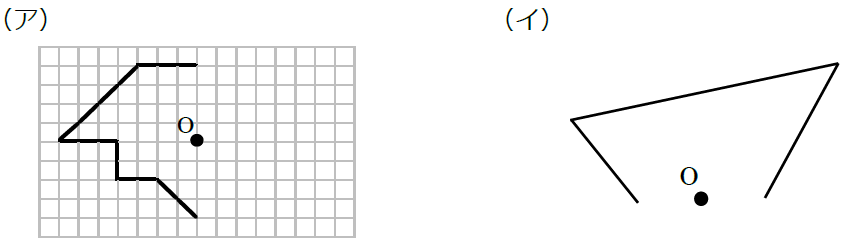



中1数学 点対称な図形とは まなビタミン




さらに複雑な図形へ Vitroid Note



高校入試 英語 数学 学習 線対称と点対称




6年算数対称な図形2 正多角形教え方



Http Www Nishitokyo Ed Jp E Sakae Life Rinji Kadai Kadai06 Files Sansu 6 Kotae Pdf
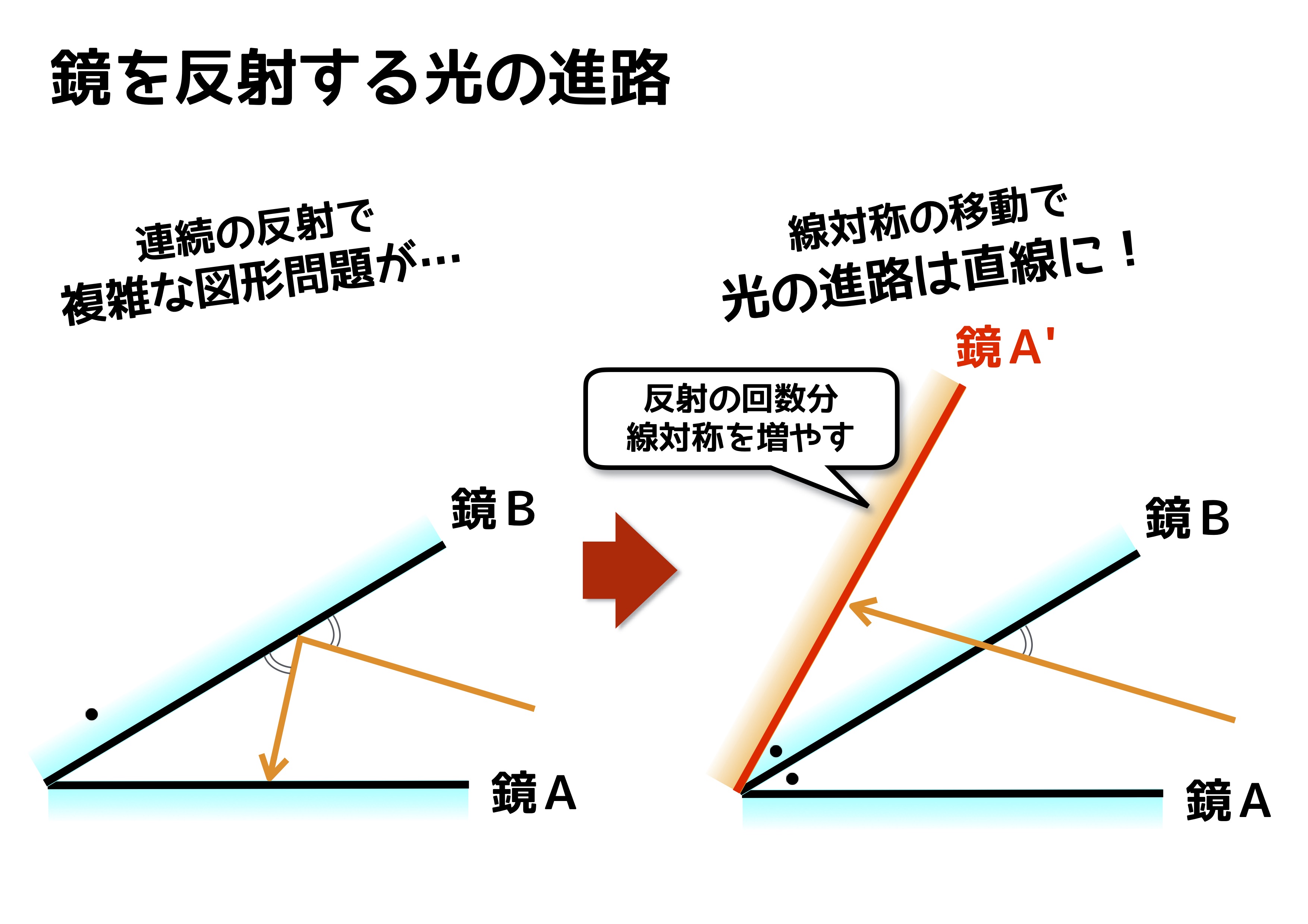



線対称と点対称 3つの性質を上手に使えるかどうかで得点に大きな差が出る 中学受験ナビ
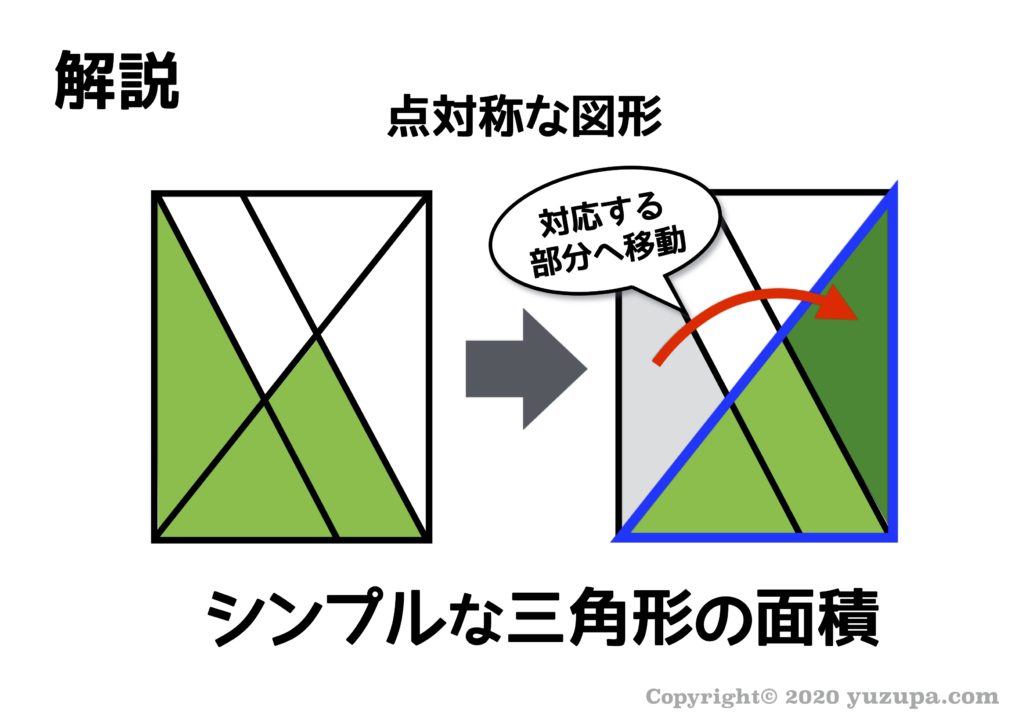



中学受験 図形の面積問題は 7つ道具 で攻略 かるび勉強部屋




特殊な定規の使い方 対称定規 定規 機能解説 トラの巻 Illuststudio 使い方講座 Clip Studio 創作応援サイト




天才ドリル 線対称 レビュー 口コミ 三歳児健診の積み木でつまずいた発達凸凹息子の努力を見よ キャッカンシ
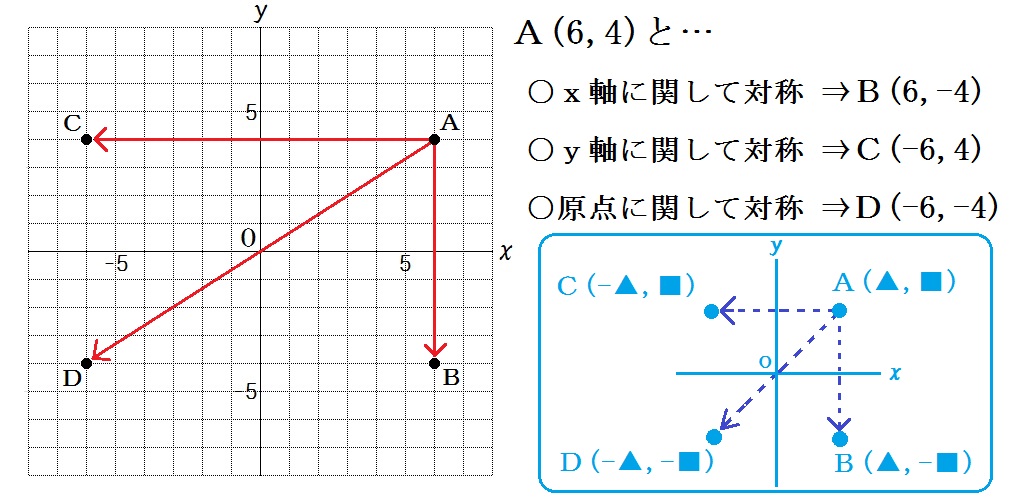



中学数学 比例と反比例 の教え方 座標とグラフ



点対称な図形の 対称の中心はそれぞれの対応する点を結んだ線分を二等 Yahoo 知恵袋



6年算数線対称点対称図形 わかる教え方



白い背景の上の円形幾何学的な対称のパターン複雑で詳細な図形のような花の説明 のイラスト素材 ベクタ Image 5716



Math 点対称な図形のかき方 働きアリ



点対称な図形
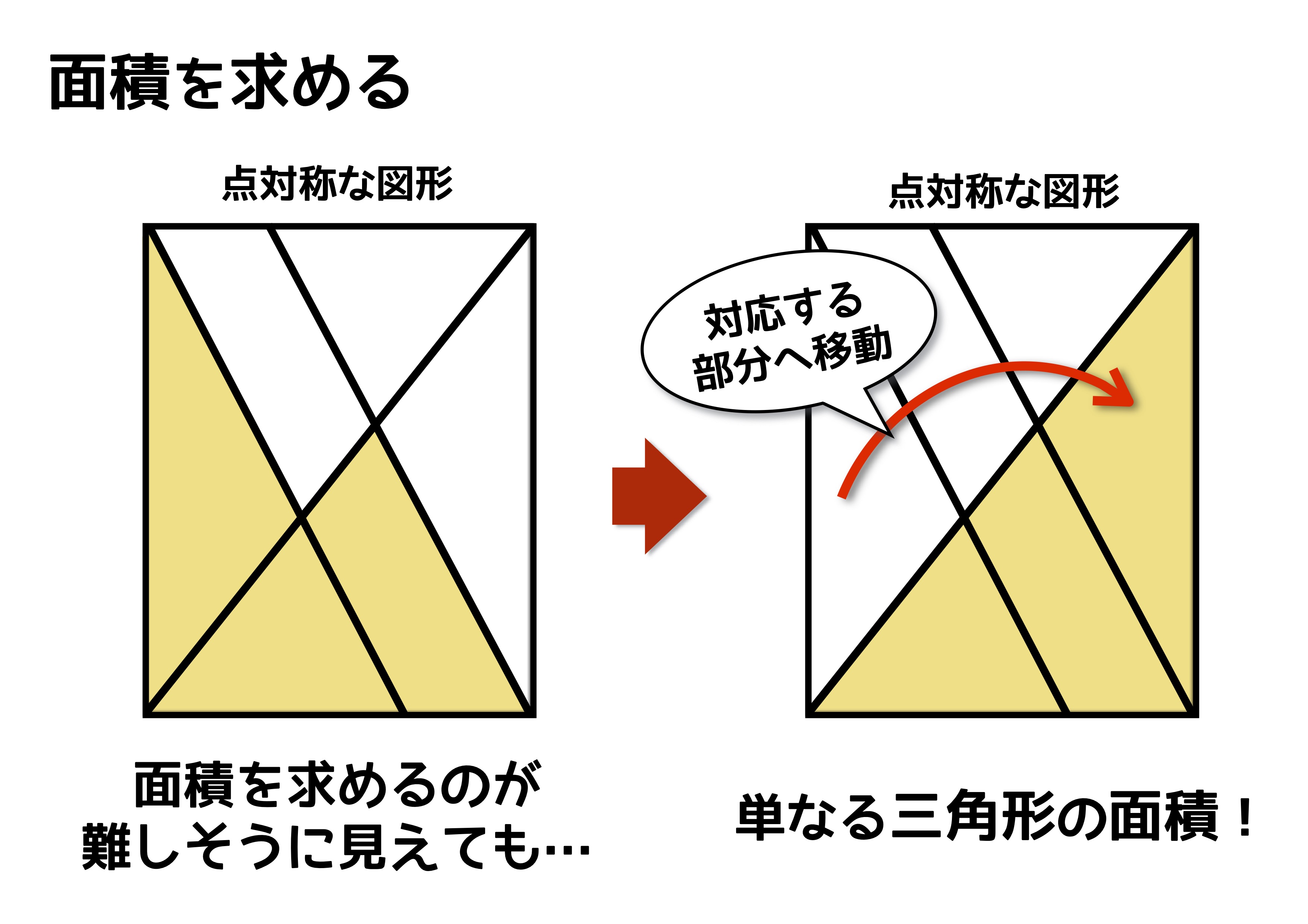



線対称と点対称 3つの性質を上手に使えるかどうかで得点に大きな差が出る 中学受験ナビ
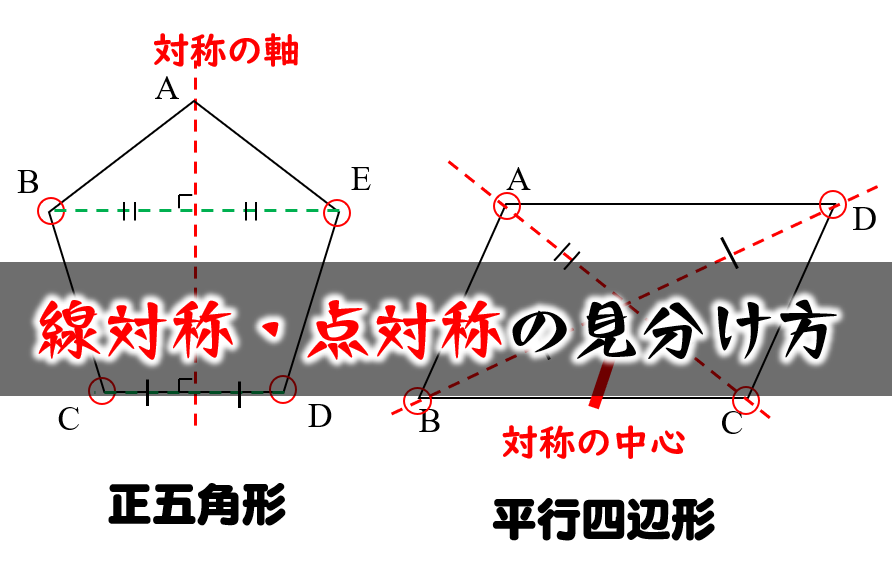



線対称 点対称の定義と違い 簡単な見分け方を解説 数学fun



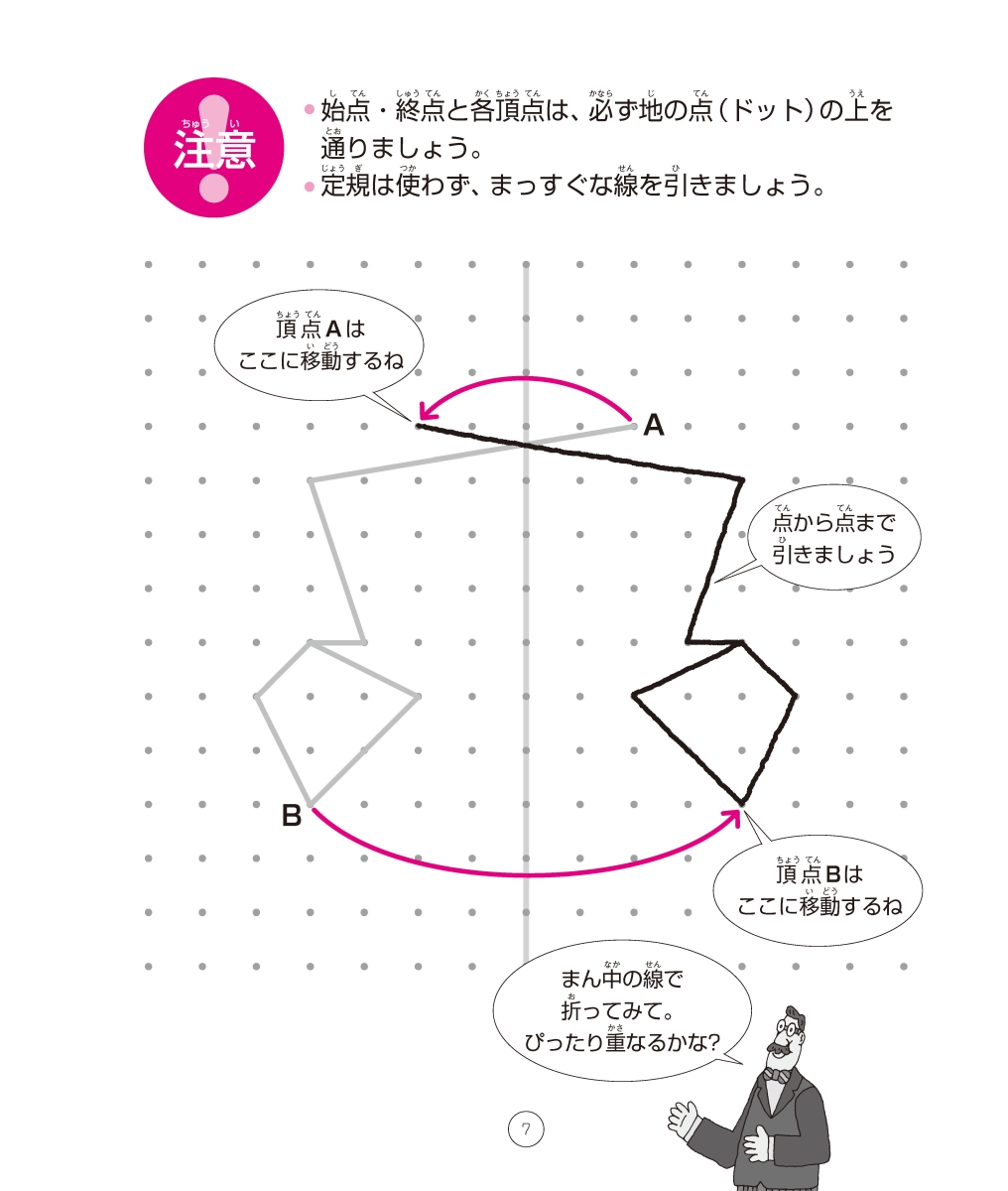
点対称な図形のかき方 Youtube



Math 点対称な図形のかき方 働きアリ The 2nd



Search Q E7 9a E5 Af Be E7 B0 81 E5 9b E5 E9 9d E7 99 81 84 Tbm Isch



楽天ブックス 考える力を育てる 天才ドリル 平面図形が得意になる点描写 線対称 小学校全学年用 算数 認知工学 本



1
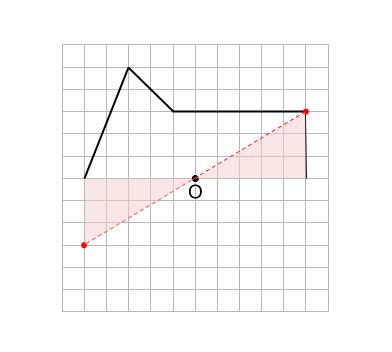



中学数学 点対称な図形 中学数学の無料オンライン学習サイトchu Su
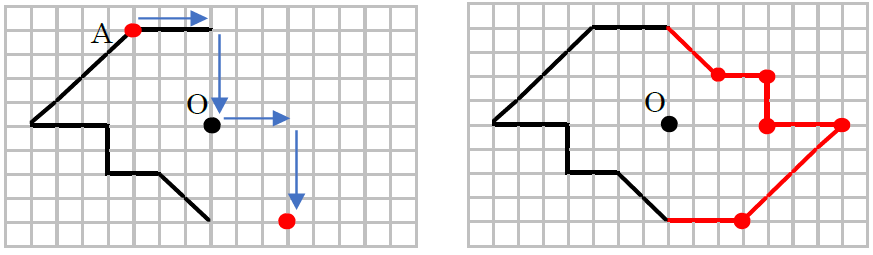



中1数学 点対称な図形とは まなビタミン




悩みのタネ 解決編 線対称と点対称 声に出さないけど思っていること




点対称な図形を書く



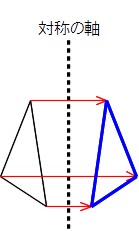
線対称 点対称の定義と違い 簡単な見分け方を解説 数学fun



1



Http Syou Oita Ed Jp Hita Kangi Files 62bde7776f21e44d32b0d4aca Pdf




世界一分かりやすい算数 小6 対称な図形




8 31まで おためし問題集特典つき 天才ドリル 平面図形が得意になる点描写 線対称 小学校全学年用 算数 考える力を育てる 認知工学 本 通販 Amazon



Http Www Nishitokyo Ed Jp E Sakae Life Rinji Kadai Kadai06 Files Sansu 6 Kotae Pdf



堺市立西百舌鳥小学校 のホームページ



四日市市立三重小学校 パブリックスペース



線対称との違いは 点対称 な図形を理解しよう お役立ち情報ページ 個別指導の学習塾なら個別指導塾スタンダード



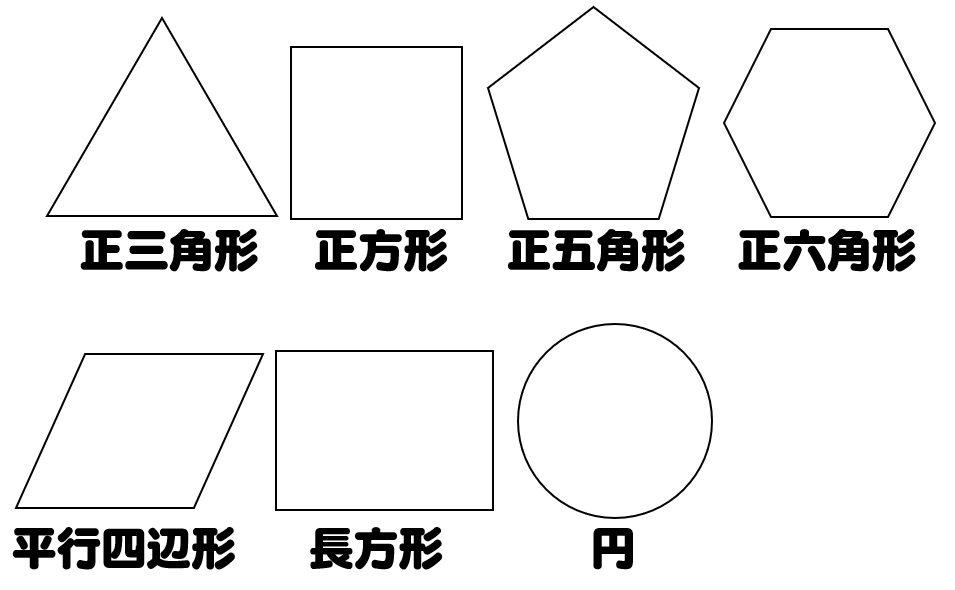
算数の点対称のことについてです 長方形正方形ひし形正六角形正八角形二等 Yahoo 知恵袋



6年算数線対称点対称図形 わかる教え方



Math 点対称な図形のかき方 働きアリ




Motoo Tange S Blog 対称性の数学



高校入試 英語 数学 学習 線対称と点対称



小学6年生の算数 点対称な図形 問題プリント ちびむすドリル 小学生
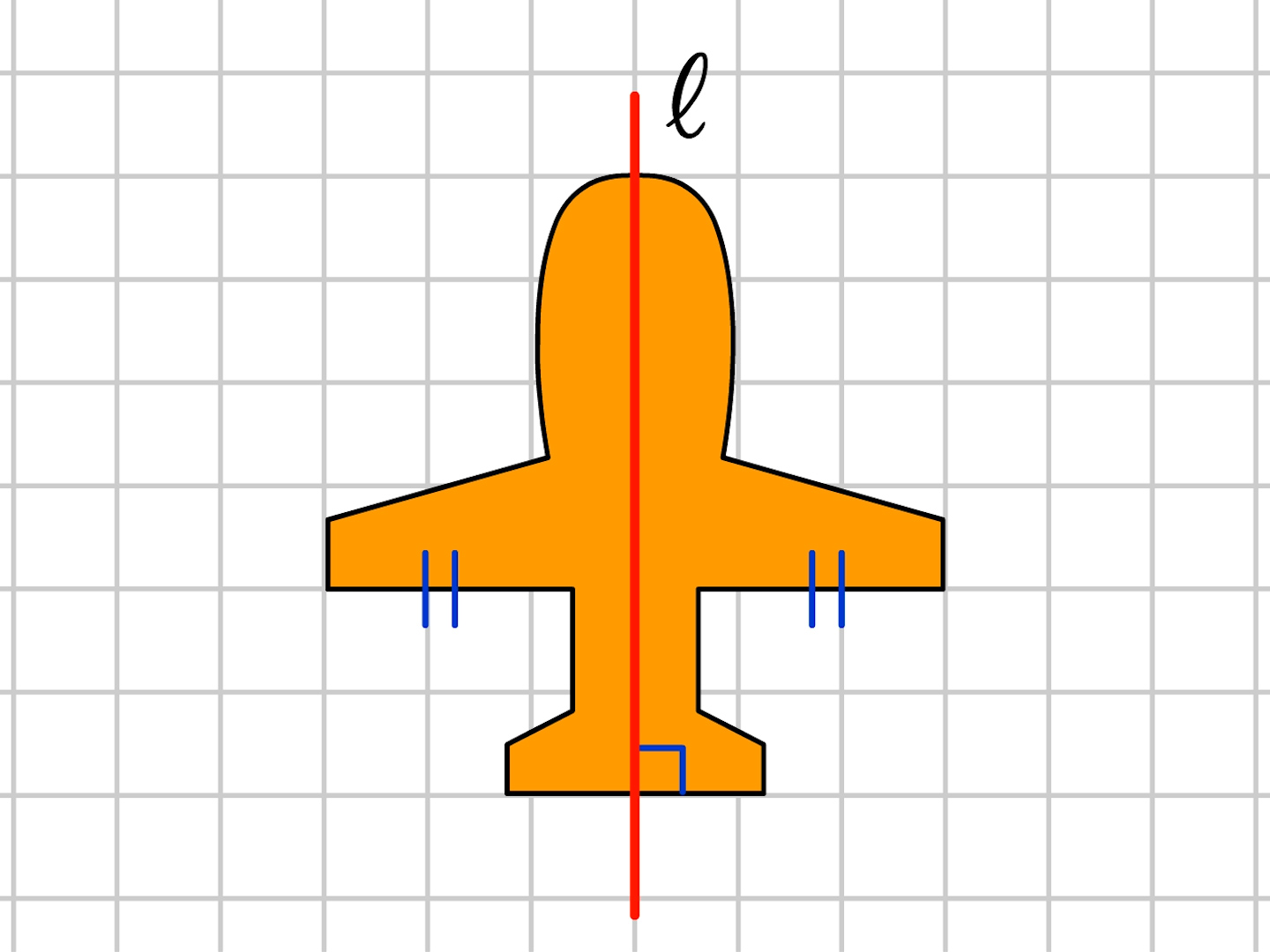



6年 線対称な図形 算数イメージ動画集 大日本図書
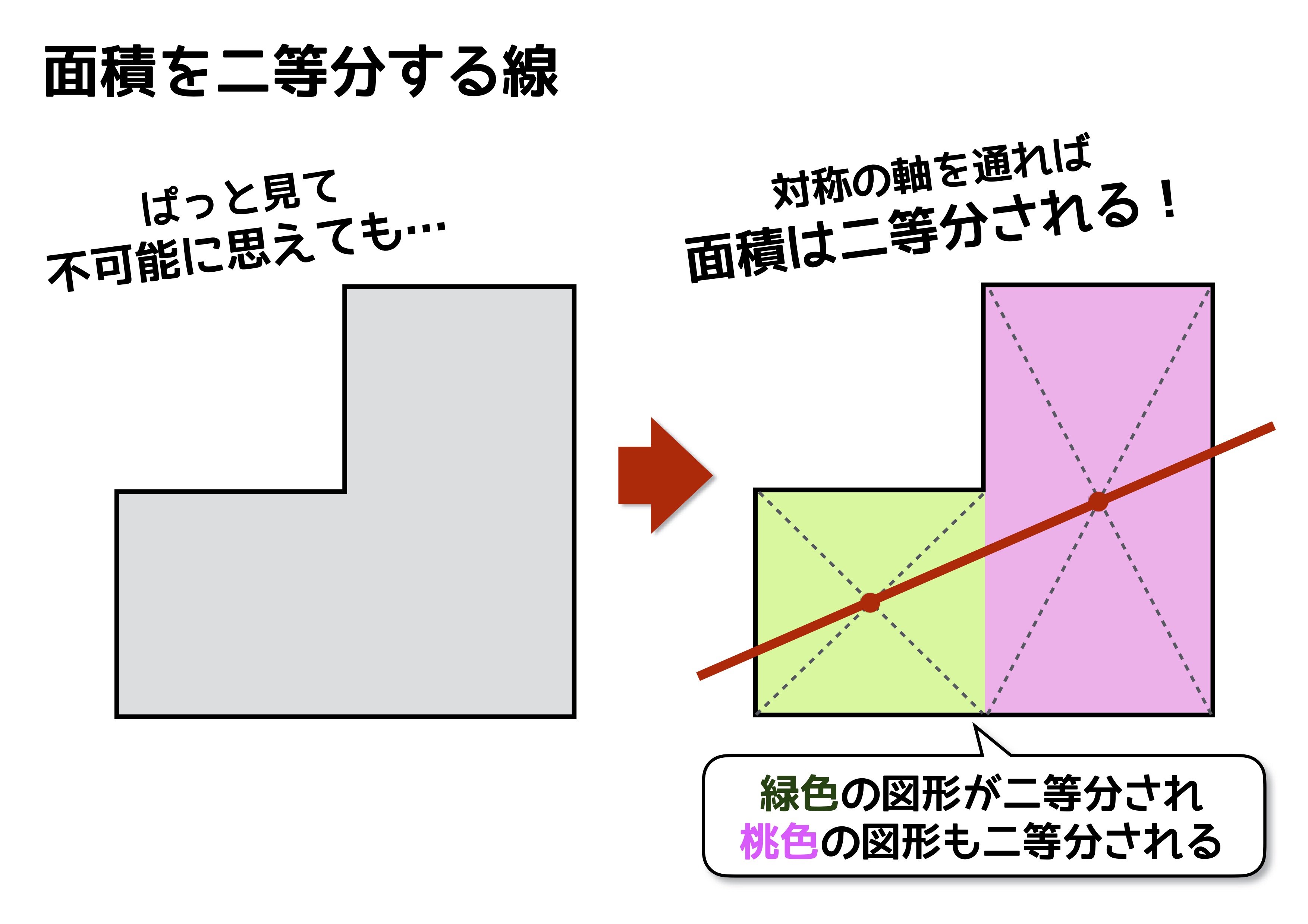



線対称と点対称 3つの性質を上手に使えるかどうかで得点に大きな差が出る 中学受験ナビ
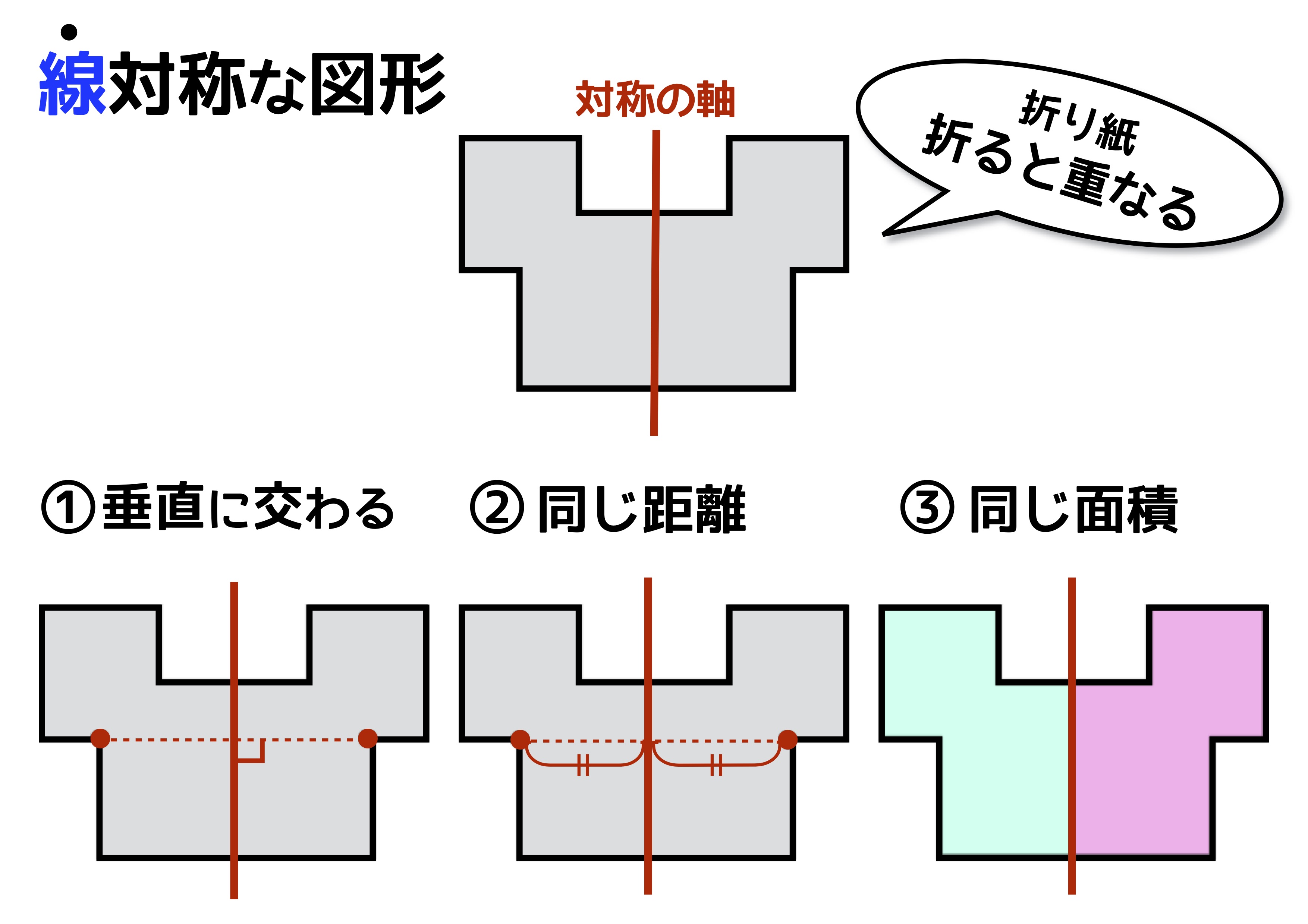



線対称と点対称 3つの性質を上手に使えるかどうかで得点に大きな差が出る 中学受験ナビ
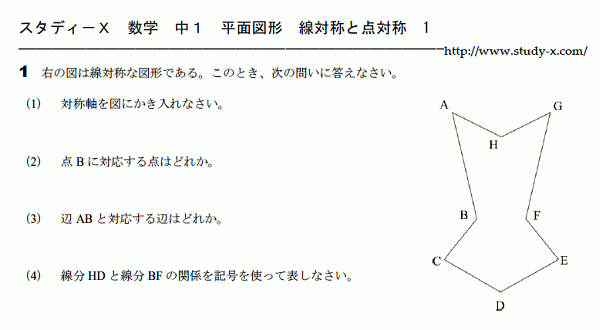



中学 数学 問題 無料学習プリント教材




6年算数 対称な図形 9時間目 いろいろな図形を対称の見方で調べよう Youtube



線対称な図形の作図 例 デジタル教科書 電子教科書
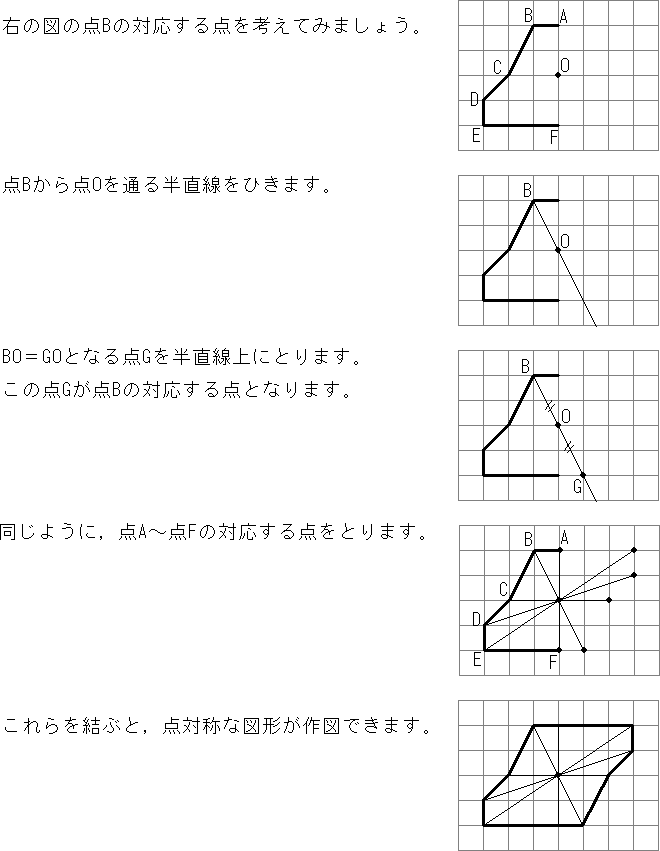



点対称な図形のかき方 中学数学 定期テスト対策 ベネッセ教育情報サイト
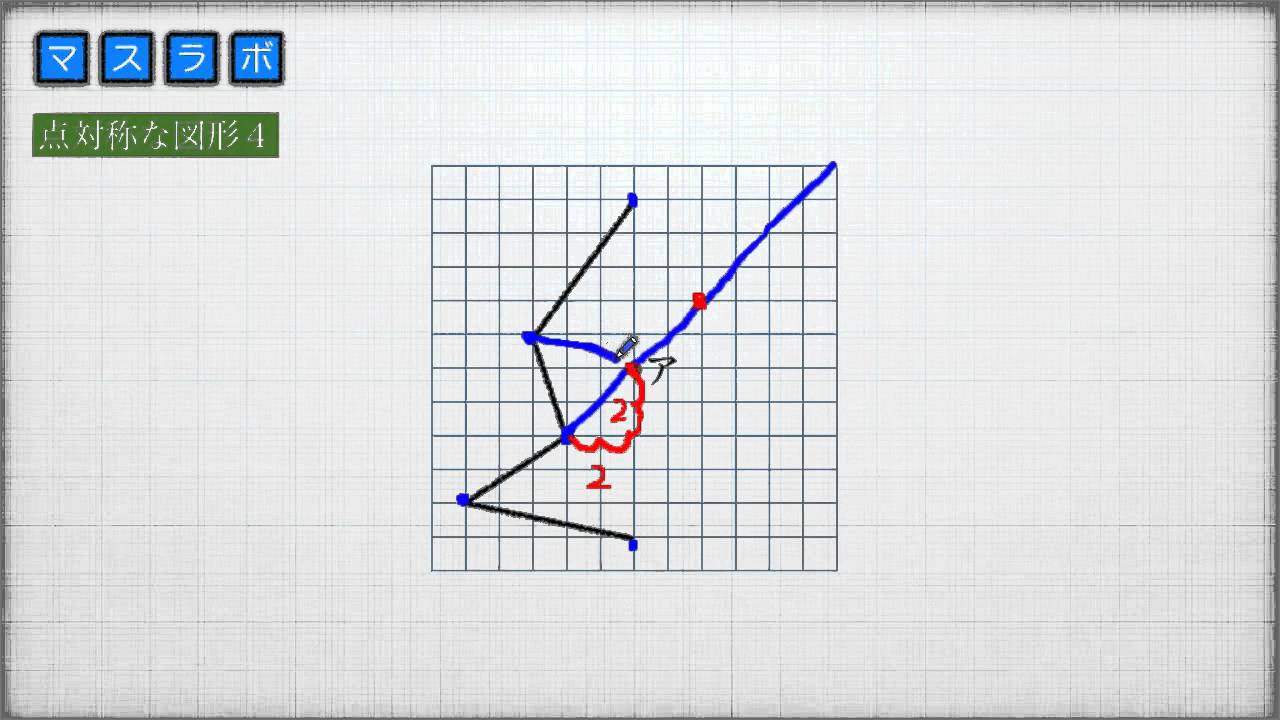



小学校6年 点対称な図形4 点対称な図形をかいてみよう Youtube
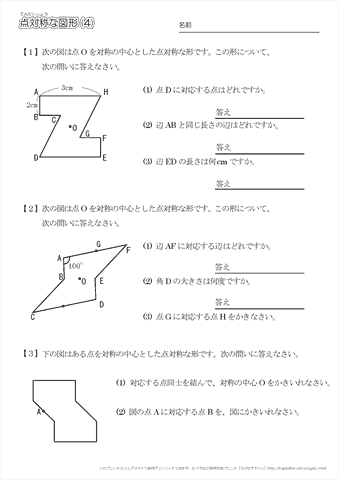



小学6年生の算数 点対称な図形 問題プリント ちびむすドリル 小学生
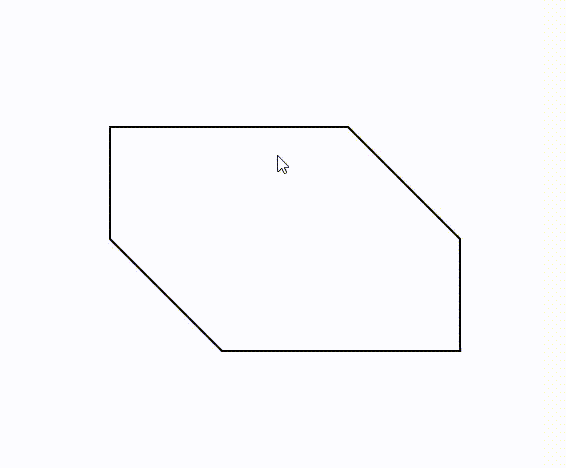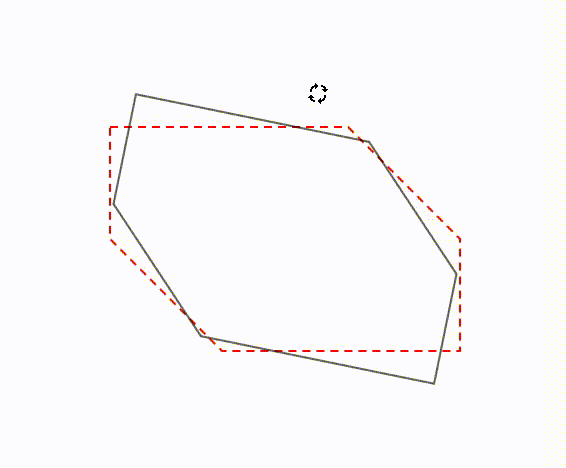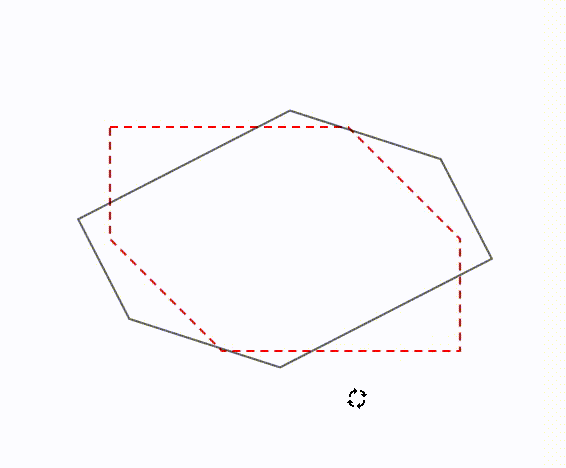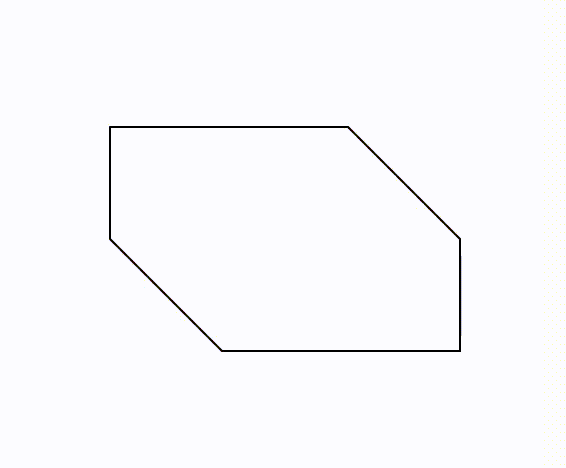



線対称 点対称の定義と違い 簡単な見分け方を解説 数学fun



Http Www Nishitokyo Ed Jp E Sakae Life Rinji Kadai Kadai06 Files Sansu 6 Kotae Pdf



1



四日市市立三重小学校 パブリックスペース



堺市立西百舌鳥小学校 のホームページ



2



高校入試 英語 数学 学習 線対称と点対称




楽天ブックス 考える力を育てる 天才ドリル 平面図形が得意になる点描写 線対称 小学校全学年用 算数 認知工学 本



小学6年生の算数 線対称な図形 問題プリント ちびむすドリル 小学生



Www City Ome Tokyo Jp School Daishi E Resources Content 738 1915 Pdf



対称な図形と授業運営 教育考現学



6年算数対称な図形2 正多角形教え方
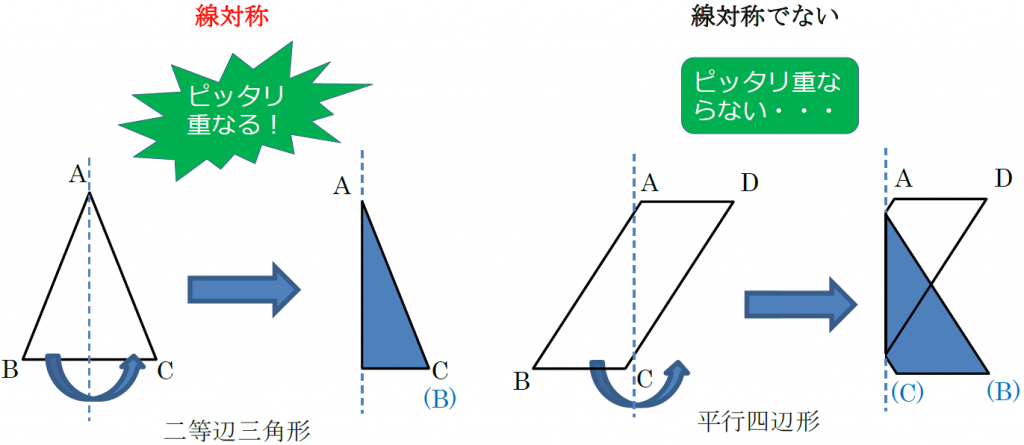



中1数学 点対称な図形とは まなビタミン
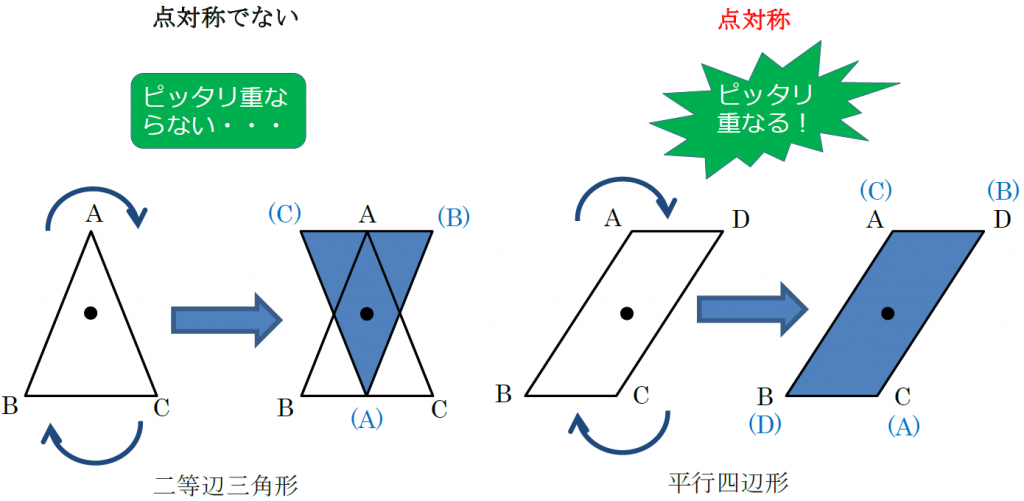



中1数学 点対称な図形とは まなビタミン



Math 点対称な図形のかき方 働きアリ
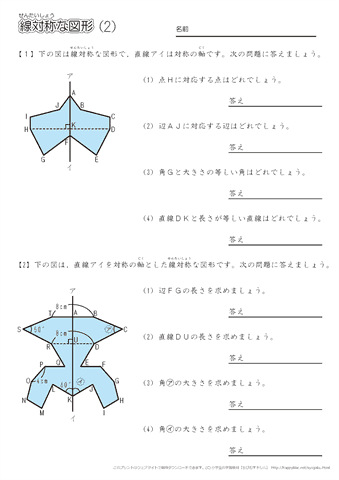



小学6年生の算数 線対称な図形 問題プリント ちびむすドリル 小学生
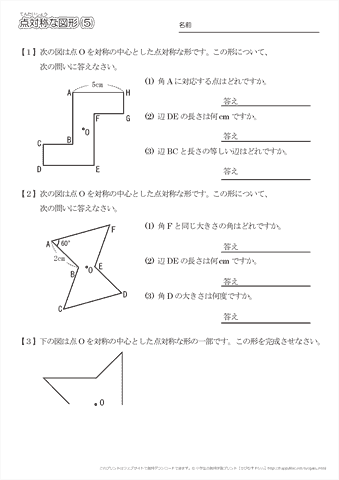



小学6年生の算数 点対称な図形 問題プリント ちびむすドリル 小学生



Www Ed Kagawa U Ac Jp Kyoshoku Kyouka Files E5 B0 8f6 E7 Ae 97 E6 95 B0 Pdf



対称な図形 4 点対称の中心はどこにあるか



点対称な図形の対応する頂点を確認する Ipadとiphoneで教師の仕事をつくる



Http Www Nishitokyo Ed Jp E Sakae Life Rinji Kadai Kadai06 Files Sansu 6 Kotae Pdf
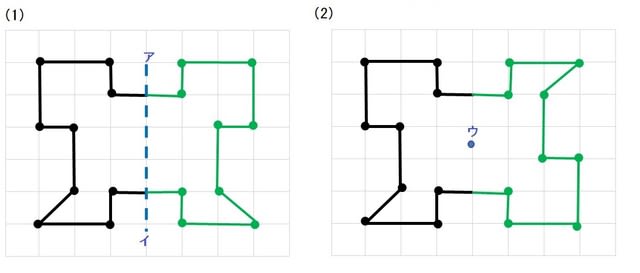



何かと教えづらい 線対称 点対称 小6 算数の教え方教えますmother S Math Happy Study Support




小6長女 算数 線対称と点対称 予習 ゆるい教育ママの育児日記




悩みのタネ 解決編 線対称と点対称 声に出さないけど思っていること



Math 点対称な図形のかき方 働きアリ The 2nd




8 31まで おためし問題集特典つき 天才ドリル 平面図形が得意になる点描写 線対称 小学校全学年用 算数 考える力を育てる 認知工学 本 通販 Amazon



対称な図形 3 点対称



放送予定 さんすう刑事ゼロ Nhk For School


