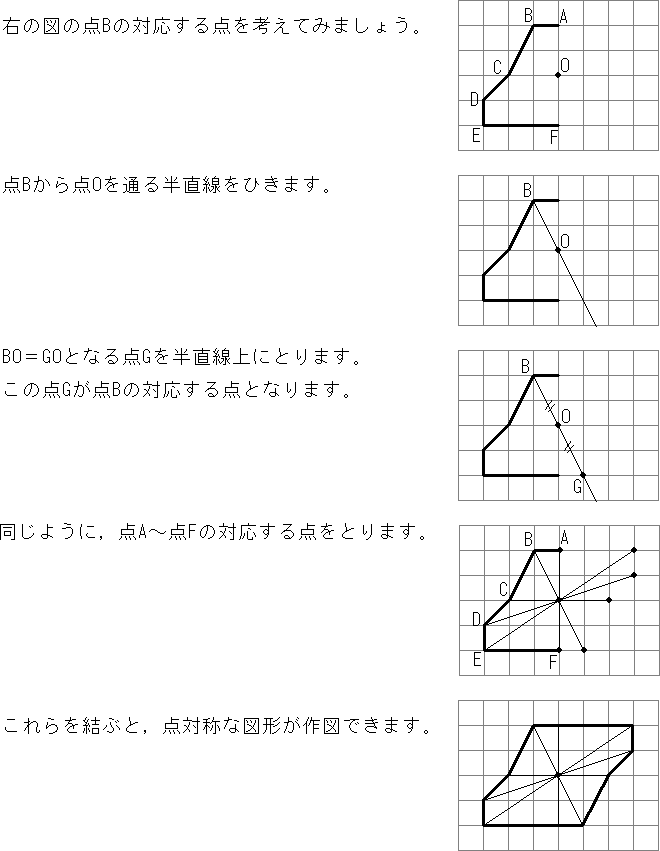
平面上で,図形を一定の方向に,一定の長さだけずらし て,その図形を移すことを平行移動という。 abc, def で点a とd,b とe,c とf が対応し ている。a を右方向に8,下方向に1 移動させた点がd である。b,c もそれぞれ同様に,右方向に8,下方向に86 対称な図形 解答 ほっかいどうチャレンジテスト 単元別問題 1 線対称 2 点対称 4 線対称 対応する2つの点を結ぶ直 線は対称の中心を通ります。 1本の直線を折り目 として2つに折ったと き、折り目の両側がぴ ったりと重なる図形を 線対称な図形といいま す。小6算数1学期 4月1対称な図形① なまえ 1 下の図で,直線アイを対称の軸とする形はどれか。正しいものを1つ選び なさい。 2 右の図は線対称な形である。直線アイを対称の軸と したとき,頂点Cに対応する頂点は( ),辺

世界一分かりやすい算数 小6 対称な図形
対称な図形 テスト
対称な図形 テスト-①対称な図形 p12 1 ①線対称 p14 1 p14 2 p16 6 p17 8 ②点対称 p18 1 p18~19 2 p 6 p21 8 ③多角形と対称 p22~23 1 p23 2対称な図形の観察や構成を通して,その意味や性質を理解し,図形に対する感覚を豊かにする。 (関心・意欲・態度)・対称な図形の美しさに気づき,身の回りから対称な図形を見つけようとする。 13 ・総括テストをする。
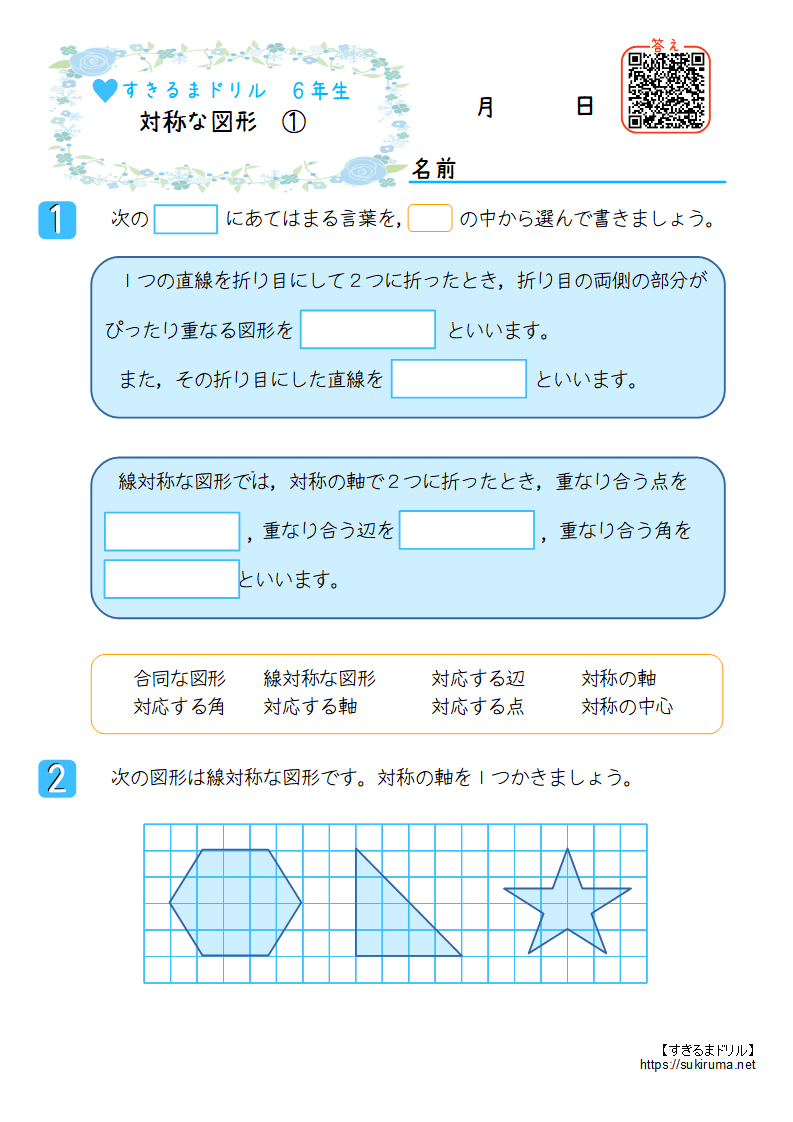



すきるまドリル 小学6年生 算数 対称な図形 無料学習プリント すきるまドリル 無料学習プリント
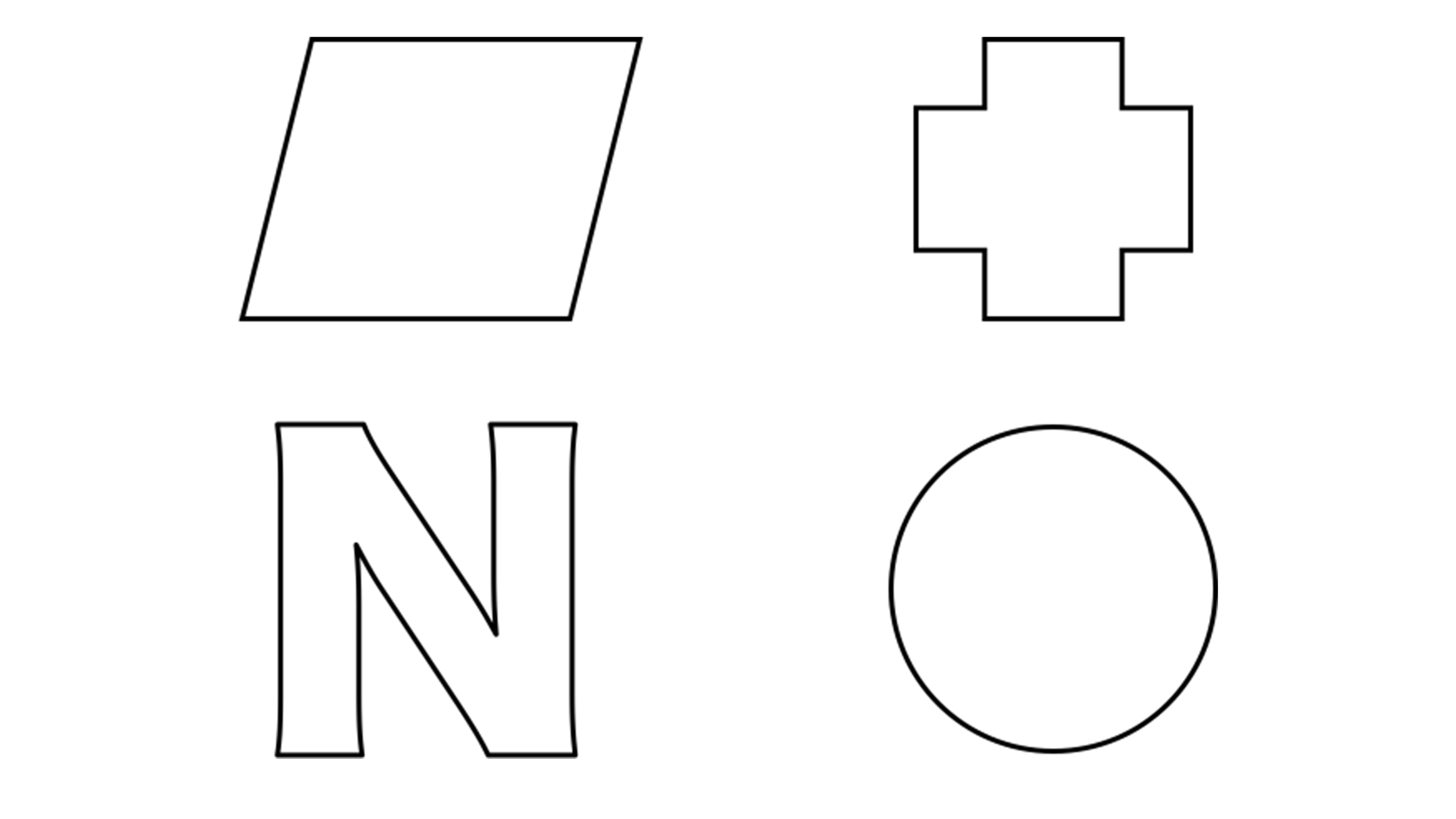
6年「対称な図形」 氏名 1 次の図形から,点対称な図形と線対称な図形を答えましょう。 線対称な図形 点対称な図形 2 下の図は線対称な図形です。 ⑴ 対称の軸は,どれですか。 ⑵ 点Fに対応する点①ある図形が,線対称,点対称 であるかどうかを判断し,説 明することができる。 ②平面図形を,対称性の観点か ら分類・統合することができ る。 ③線対称,点対称な図形の性質 や3つの移動における性質 を,用語・記号を用いて表す ことができる。世界一分かりやすい算数 小6 「対称な図形」 教科書の内容に沿った算数プリント問題集です。 授業の予習や復習にお使いください! また、各単元の最後にまとめテストもあります。 PDF形式ですべて無料でダウンロードできます。
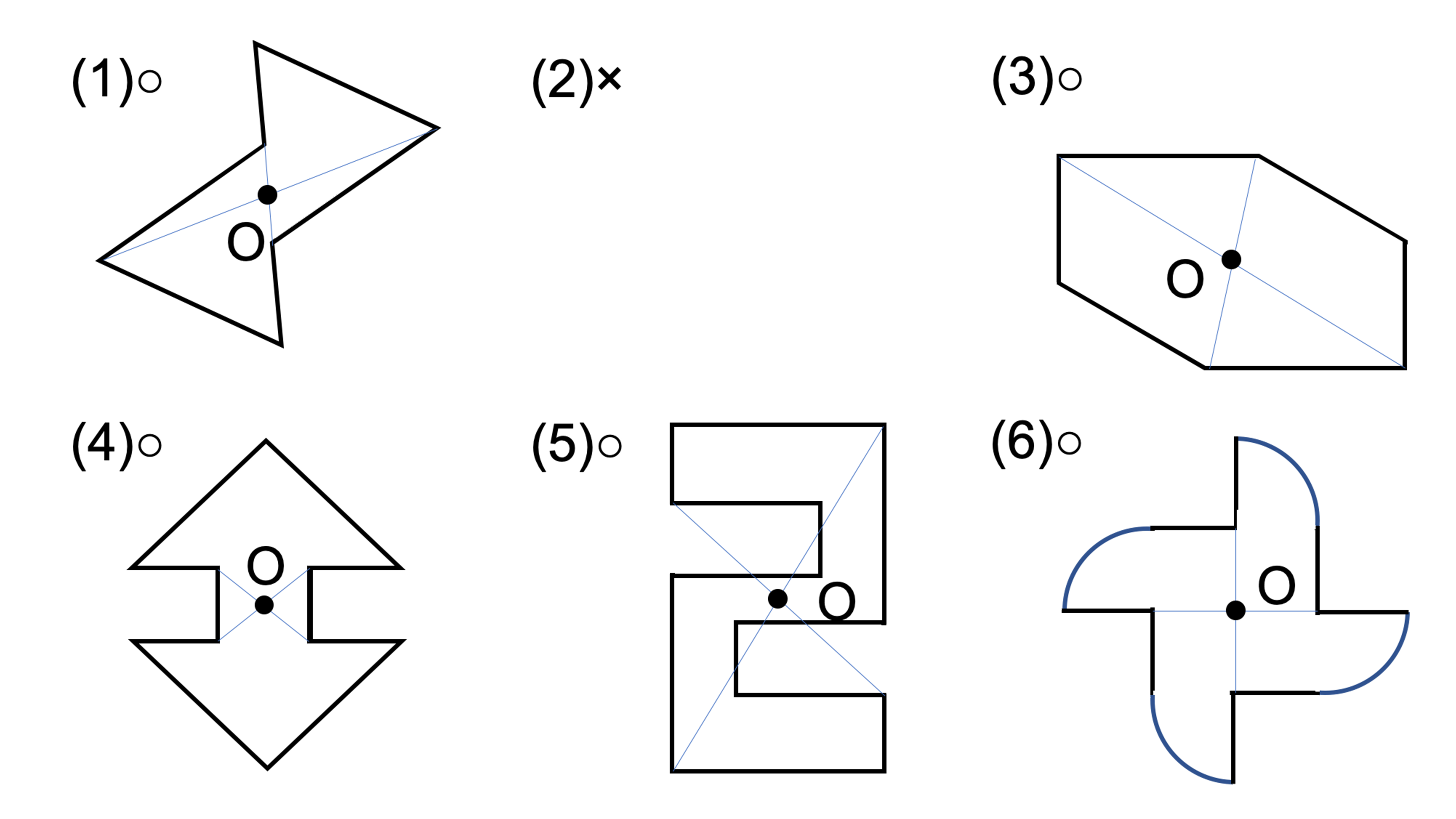
6年1学期 一括ダウンロード ワークシート PDF ︎ 17MB 解答 PDF ︎ 17MB PDFファイルは,クリックすると内容を別ウィンドウに表示します。 ダウンロードに際しましては,あらかじめ 免責事項 をご確認ください。 ゲシュタルト原則(ゲシュタルトの法則) Gestalt principles (Gestalt laws) 人間がゲシュタルト(形態)を見る際に、全体像から見て近くに並んでいるものを無意識にグループとして理解したり、閉じているものをセットで認識する傾向を言う。 「ゲシュタルト鬼っ子チャレンジテスト 6年 R3・1-⑥ 対称な図形 名前( ) 1 下のような四角形があります。 線対称な図形や点対称な図形には を,そうでないものには×をつけましょう。
図形・空間認識に関する一考察 八雲高等学校 吉田 奏介 1 / 9 §11 数学教育から見た図形・空間領域 大分大学教授の川㟢道広氏は図形感覚と図形概念を次のように示している。(*1 に 図 形 感 覚 外的感覚:外的な対称そのものを 捉え、どのような図形で小学6年生の算数 点対称な図形 問題プリント 関連する学習プリント ★教科書ぴったりトレーニング コラボ教材★ 小学1~6年生 算数 確かめのテスト解説動画付きウ 対称な図形の意味や性質に気付かせるために,実際に線対称な図形を折り曲げて重ねてみた り,回転させてみたりしながら,実感を伴って図形の対称性を感じられるようにする。 調査1右の図形はどのよう な特徴があるか説明しなさい。




小学6年算数 対称な図形 活用できる教材公開 アルファベットで対称な図形を探してみよう Math Channel Note




対称な図形 小学生 算数のノート Clear
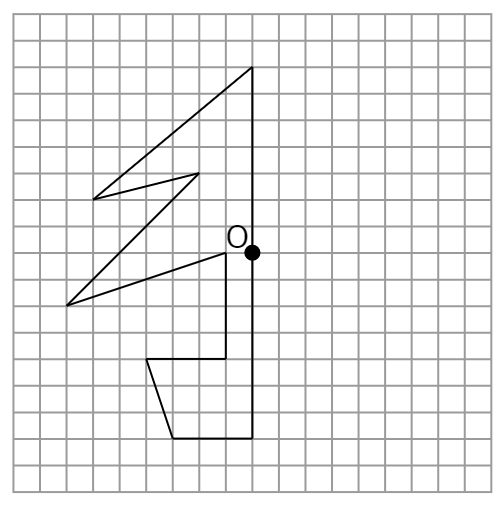
1枚の折り紙を数回折り、最後にハサミで一部を切り取ります。 広げた後、折り紙がどのような図形になっているかを問う問題です。 頭の中だけで考えるのは難しいですが、「線対称」を使えばとてもカンタンです! (*´∀`*) 問題1(線対称) 問題2(線無料 中1数学 テスト対策問題 問題プリント 平面図形1 直線と角・対称 テキスト マスコン 中1数 テスト対策問題 (平面図形1 直線と角・対称) 氏名 ( )TQ125 (1124) 次の ( )にあてはまることばを入れよ。 (1128) 次の①,②を三角定規を使ってかきなさい。 ① 直線3 次のような図形をかきましょう。 ① 直線ABが対称の軸となるような線対称な図形 ② 点Oが対称の中心となるような点対称な図形 4 次の㋐~㋔の図形について,あとの問いに答えましょ う。 ㋐ 平行四辺形 ㋑ 正三角形 ㋒ 正方形



点対称な図形のかき方 中学数学 定期テスト対策 ベネッセ教育情報サイト




小6算数 対称な図形の折り紙 ブログ アビット
簡単に点対称・線対称で落書きするツールをHTML5版にしてみるテストです。 Tweet Animate CCHTML5 ツール 前の記事 ミニドット絵メーカーHTML5版 移植テスト 次の記事 アバター画像合体ツール for pictSQUARE(仮)1 対称な図形 学 年 組 氏 名 1 次の文字について,線対称な形には ,点対称な形には ,どちらでもないときは× を答えましょう。 線対称な形とは,1本の直線を折り目にして二つ折りにしたとき,両側の部分がぴったりと重なる形です。点対称な形線対称な図形をかきましょう。 次の図形の名前をかきましょう。 ① 線対称にはなっていないが,点対称になっている四角形 ② 線対称にも点対称にもなっており,対称の軸の数が8本の正多角形 4 ② 下の点対称な図形に対称の中心を かき入れましょう。



中1数学 点対称な図形とは まなビタミン
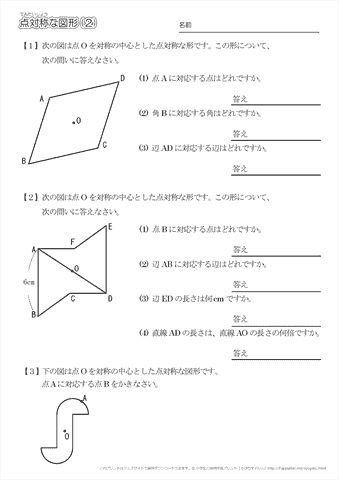



小学6年生の算数 点対称な図形 問題プリント ちびむすドリル 小学生
1年数学第5章平面の図形単元テスト h2132 ※途中のコンパスの線などは必ずこの答案に残しなさい。 1年()組()番名前() 1次の()にあてはまる言葉などを答えなさい。ただし, 漢字の部分は漢字で書きなさい。知識理解(2点×14)鬼っ子チャレンジテスト 6年 R3・1-⑥ 対称な図形 ( 解 答 例 ) 1 下のような四角形があります。 線対称な図形や点対称な図形には を,そうでないものには×をつけましょう。① 対称な図形 ・HP掲載教材「自己評価テスト6年 1対称な図形」 ・教科書QR p10「じゅんび(対称な図形)」 ・教科書QR p15「都道府県のマーク(線対称)」 ・教科書QR p19「地図記号(点対称)」 ・教科書QR p24「たしかめよう(対称な図形)」 2文字と式




点対称な図形 問題プリント まとめテスト 小学6年生用無料算数プリント




小5長女 算数 線対称と点対称 予習 ゆるい教育ママの育児日記
15 rijen 6学年 わくわく算数自己評価テスト(児童配布用資料) テスト 単元名(上巻) テスト 単元名(下巻) 1 対称な図形 1KB 9 比例と反比例 233KB 2 文字と式 193KBサンパズ! 6年生プリント目次 分数のかけ算とわり算と逆数 対称な図形と円の面積 文字を使った式と比 速さ・道のり・時間 応用プリント チャレンジプリントダウンロード小学生の算数・図形・面積・体積に関する算数の問題プリント、練習プリントです。 無料でダウンロード、印刷してご利用いただけます。 小学1年生の算数 図形 練習問題プリント 小学2年生の算数 図形 練習問題プリント 小学3年生の算数 図形 練習問題




すきるまドリル 小学6年生 算数 対称な図形 無料学習プリント すきるまドリル 無料学習プリント
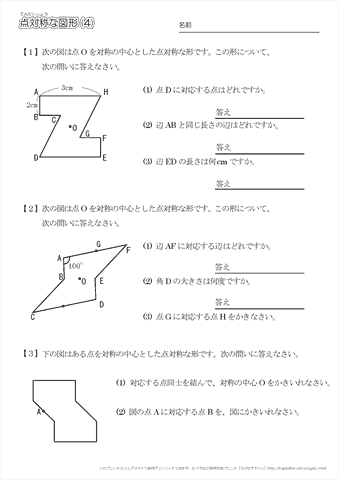



小学6年生の算数 点対称な図形 問題プリント ちびむすドリル 小学生
_小6b_対称な図形、点対称、対称の軸、対応する点、中心を通り同距離 100 点満点 ( 合格点 設定なし ) 残り時間 テスト開始 テストを開始するには テスト開始 ボタンを押してください。 問題 1 次の図は点oを対象の中心とする点対称な図形です。下の図は、直線で2つにおるときちん と重なります。 に当てはまる言葉を書 きましょう。 ①1本の直線を折り目にして折っ山口県教育庁義務教育課 〒 山口県山口市滝町11 電話 ファックス
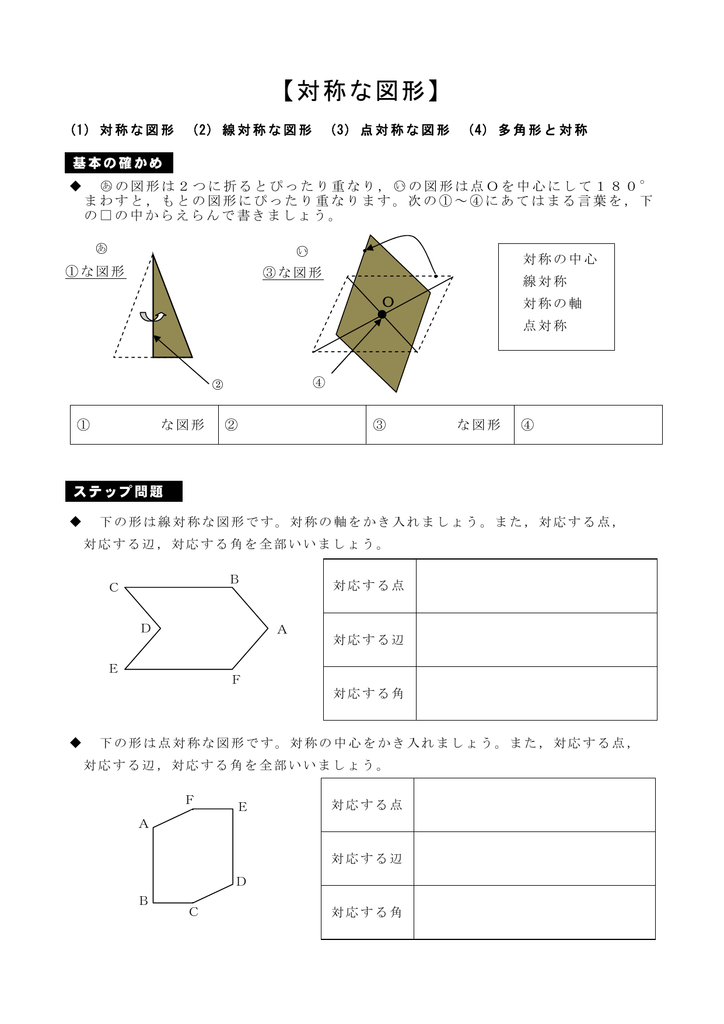



対称な図形




線対称 点対称な図形のかき方 対称な図形 小6算数 豊橋の学習塾 勉強 Youtube スタディチューブ
無料 中1数学 テスト対策問題 解答プリント 平面図形1 直線と角・対称 テキスト マスコン 中1数学 テスト対策問題 (平面図形1 直線と角・対称) 氏名 ( )TA125 (1124) 次の ( )にあてはまることばを入れよ。 (1128) 次の①,②を三角定規を使ってかきなさい。 ①下の形は点対称な図形です。対称の中心をかき入れましょう。また,対応する点, 対応する辺,対応する角を全部いいましょう。 ① 線対称 な図形 ② 対称の軸 ③ 点対称 な図形 ④ 対称の中心 基本の確かめ ステップ問題 対称の中心 線対称 対称の軸 点1 対称な図形 学 年 組 氏 名 1 下の図のようなアからクの図形について考えましょう。 ア 二等辺三角形 イ 長方形 ウ 正五角形 エ 平行四辺形 オ ひし形 カ 円 キ 正六角形 ク 正八角形 ※この他にも円の対象の軸はたくさんある。




すきるまドリル 小学6年生 算数 対称な図形 無料学習プリント すきるまドリル 無料学習プリント




小学校6年算数 1 5 点対称な図形のかき方 Cmovie 教育に特化した無料動画サイト シームービー オンライン学習サイト
算数 第6学年 対称な形 月 日 名前 問 下の3つの正多角形について,質問に答えなさい。 下の6つの図形について質問に答えなさい。!5対称の軸が2本あるのはどの図形ですか。!8点対称な図形はどれですか。!7線対称な図形はどれですか。線対称な図形では,対称の軸で2つに折ったとき,重なり合う点を 重なり合う辺を 重なり合う角を といいます。 次の図形は線対称な図形です。対称の軸を1つかきましょう。 対称な図形 ① 1 , ,図面の役割と種類 日本工業大学製図の基礎 設計者 加工・製作者 意思疎通 役割 (テキストp2) 決められたルール(規則)に従って図面を描く
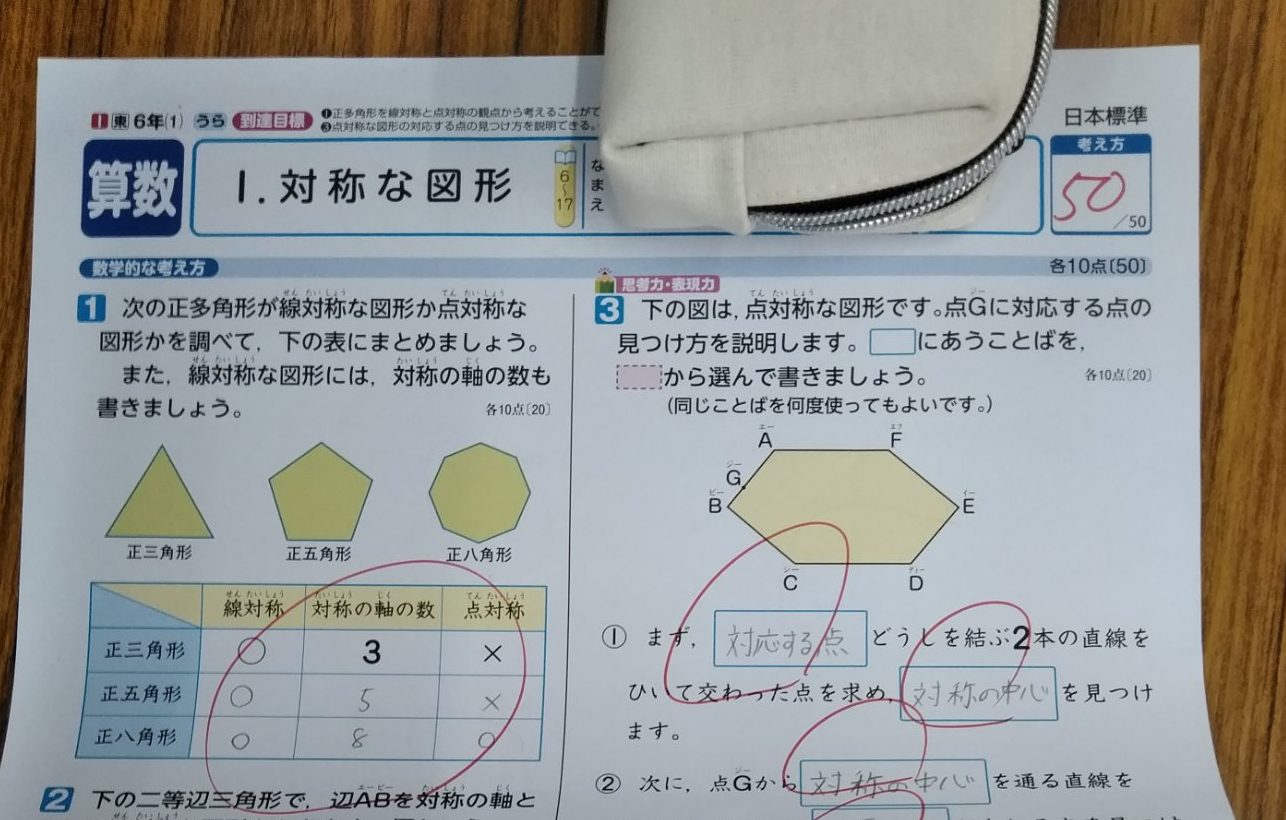



テスト対策に100点報告 完全個別指導の修優舘




世界一分かりやすい算数 小6 対称な図形
ほしいプリントのタイトルを選んでクリックまたはタップしてください 算数6年 タイトル一覧 1 対称な図形 すきるまドリル 小学6年生算数 「対称な図形」 学習問題プリント5枚な図形では,対称の軸 じく を折り目にして折 ったとき,両側の部分がぴったり重なります。 2 ①w,e,r,t ②q,w,e,t ③w,e,t "④&本 ⑤ ⑥w,e 点対称な図形では,対称の中心のまわりに!(~° 回転させたとき,もとの形にぴったり重なります。
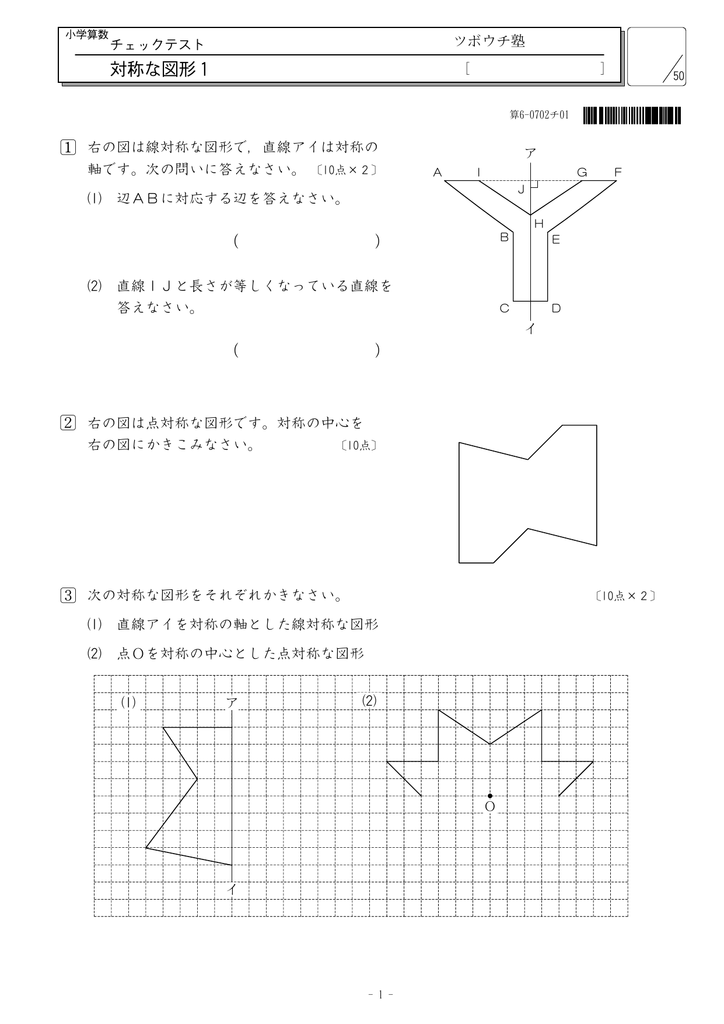



対称な図形1 ツボウチ塾



岐阜県大垣市の個別指導塾 ナビ個別指導学院大垣校ホームページ 満点




テスト対策に100点報告 完全個別指導の修優舘




6年算数 対称な図形 3時間目 線対称な図形を調べましょう Youtube
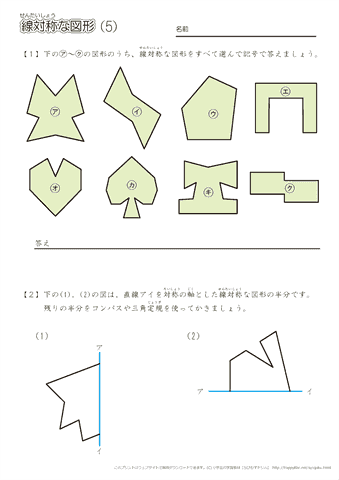



小学6年生の算数 線対称な図形 問題プリント ちびむすドリル 小学生




小6算数 対称な図形の折り紙 ブログ アビット




小学6年 算数 テスト 小学6年 算数 テスト Josimgfree




富士市 厚原にある 個別指導塾 もえぎ 初めて学校のテストで100点 おめでとう




対称な図形 Ict教材eboard イーボード




世界一分かりやすい算数 小6 対称な図形




Pdcaサイクル学習法 可児の個別専門塾 京進 きょうしん スクール ワン 可児教室



Www City Date Hokkaido Jp Hotnews Files Pdf




雑記 九大の学食と両面満点 By 福岡の私立中学 高校受験 個人契約の家庭教師ふなきのブログ
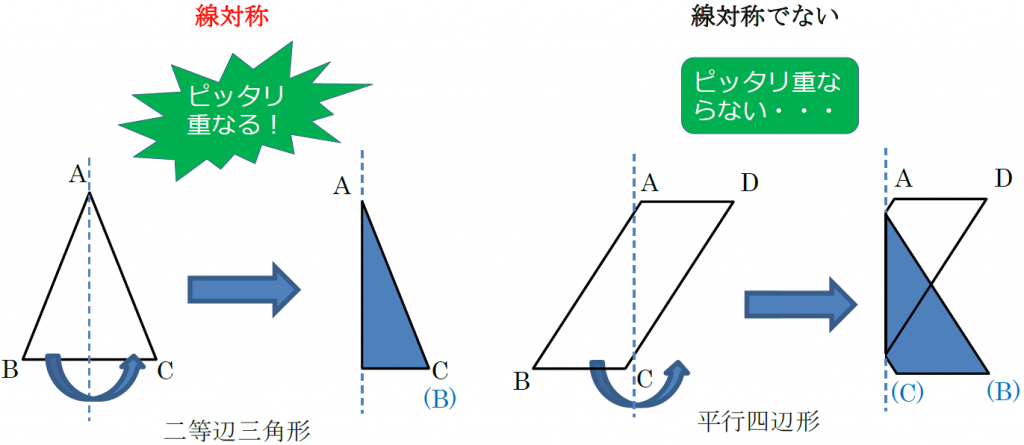



中1数学 点対称な図形とは まなビタミン




算数テスト 3兄弟ママのドタバタ日記



小学6年生tくん 点対称 確認テストも満点 学習塾 凛 Rin 静岡県浜松市東区の個人塾
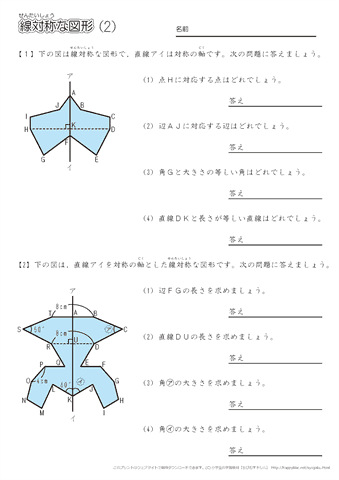



小学6年生の算数 線対称な図形 問題プリント ちびむすドリル 小学生




対称な図形 Ict教材eboard イーボード
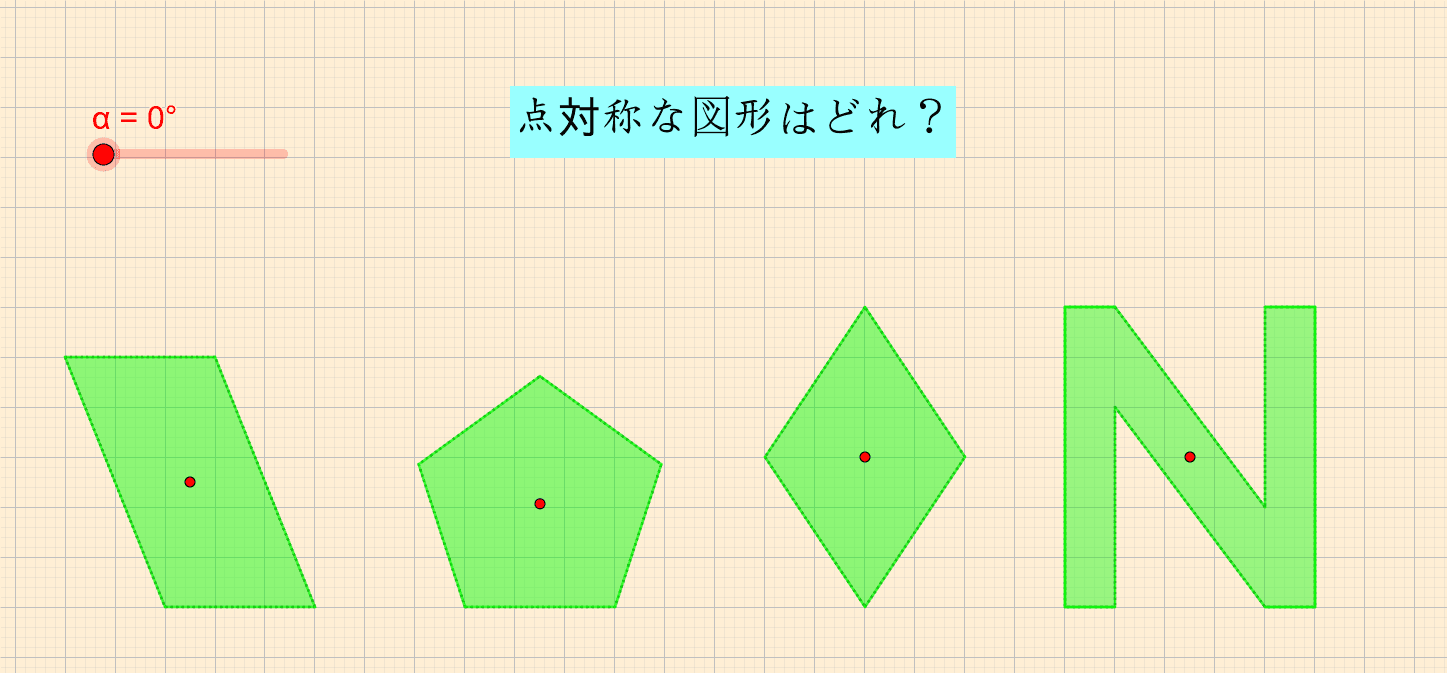



点対称な図形はどれ Geogebra



線対称 点対称な図形の書き方 中学1年数学 勉強 Youtube スタディチューブ



1



Http Www Nyushi Sugaku Com Tyu1 T1 5 E 02 Pdf



線対称な図形をコンパスで書く方法を教えていただけますか Yahoo 知恵袋
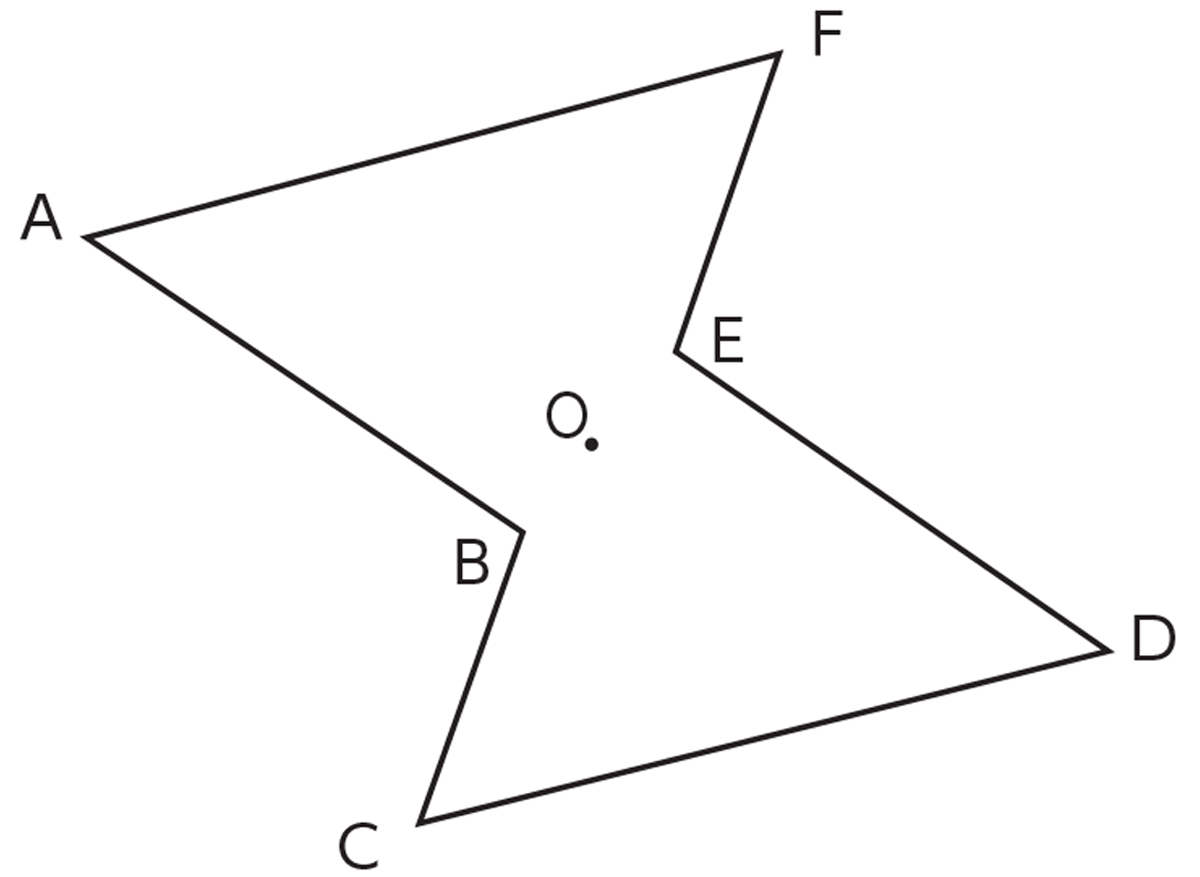



小6算数 点対称な図形の性質 指導アイデア みんなの教育技術




線対称な図形 問題プリント 対象の軸や対応する点 小6無料算数プリント



100点のテスト 岐阜の学習塾 カナン学院 カナングループ



1




線対称 点対称 算数用語集




岐南北小6年生 算数スタートダッシュ 岐阜県羽島郡岐南町の個別塾 学習塾 ナビ個別指導学院 岐南町校ブログ



Http Www Kita9 Ed Jp Eductr Handbook Challengesheet Elementaryschool Sansuu 6 600 Pdf




三津っ子日記 松山市立三津浜小学校



線対称との違いは 点対称 な図形を理解しよう お役立ち情報ページ 個別指導の学習塾なら個別指導塾スタンダード




Lihat Cara Penyelesaian Di Qanda



Fdk3a7ctb5192box5b Com Es 6nen Mt Tentaishou Sakuzu Html




算数のテストをやりました めっちゃいい点数でビビる ゚d゚ ゲームと柴犬は神




小6 算数 小6 12 対称な形 Youtube



算数の点対称のことについてです 長方形正方形ひし形正六角形正八角形二等 Yahoo 知恵袋



無料 中1数学 基本問題 問題プリント 平面図形2 多角形 点対称 135




算数の単元導入教材 対称な図形 で活用できるアルファベットで対称を探そう 小学校6年生 対称な図形 Youtube



算数 対称な図形 学校そっくりテスト かなた君満点 コロンビア塾 中学校夏休み31日まで延長
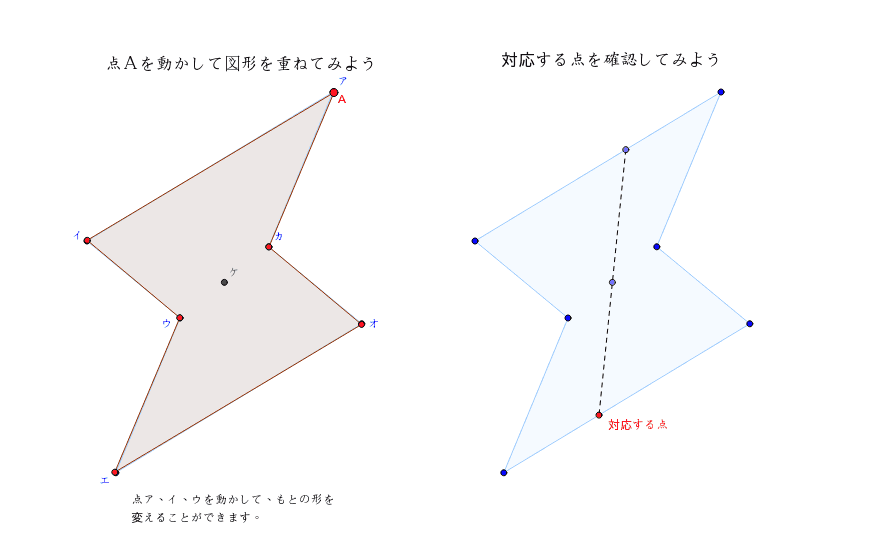



点対称な図形の観察 Geogebra




点対称の図形の書き方を教えてください Clear




6年生のみなさんへ 堀津小blog 羽島市立堀津小学校



無料 中1数学 基本問題 解答プリント 平面図形2 多角形 点対称 135




小学6年算数 対称な図形 活用できる教材公開 アルファベットで対称な図形を探してみよう Math Channel Note




โน ตของ 小6まとめ算数 復元 ช น Primary算数 Clear




平面図形 平行四辺形は線対称ではないのか 中学数学 定期テスト対策サイト




新しい個別指導s Live スクールe Live とうきょう篠崎駅前校 Home Facebook
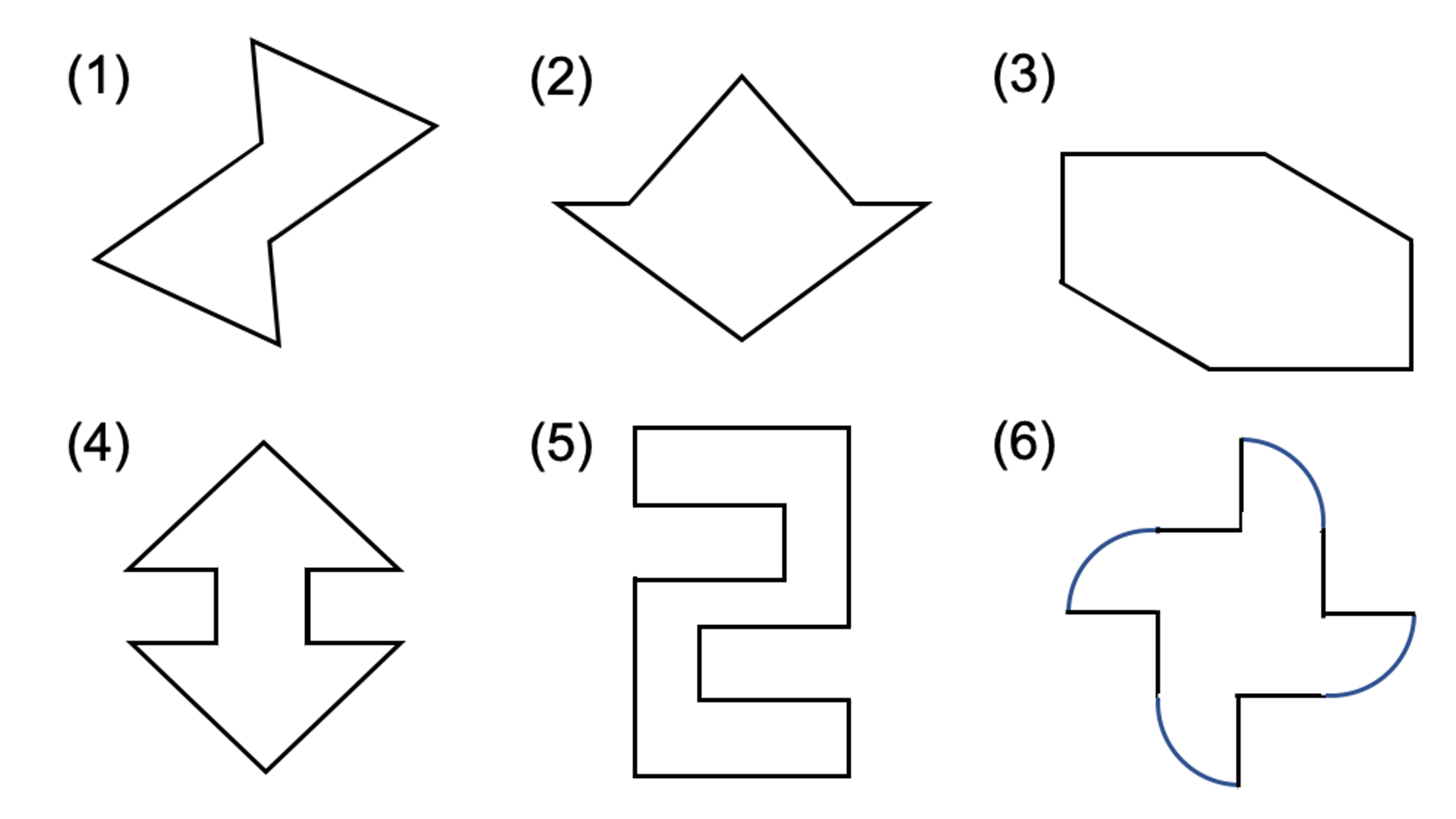



線対称との違いは 点対称 な図形を理解しよう お役立ち情報ページ 個別指導の学習塾なら個別指導塾スタンダード
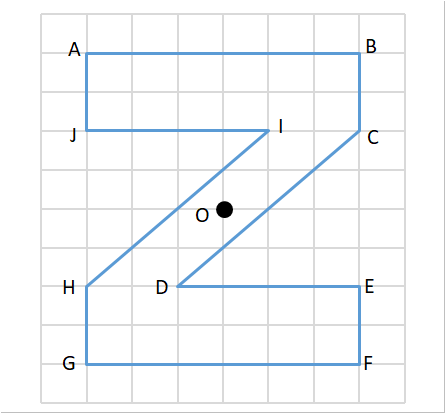



中山先習塾 練習問題 テストが作動しないときは Internet Explorerをお試しくださいワン 小6 B 対称な図形 点対称 対称の軸 対応する点 中心を通り同距離 100 点満点 合格点 設定なし 残り時間 テスト開始 テストを開始するには
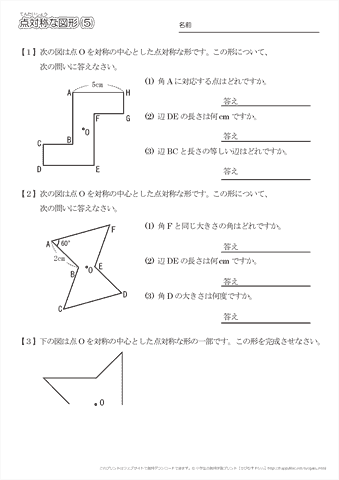



小学6年生の算数 点対称な図形 問題プリント ちびむすドリル 小学生
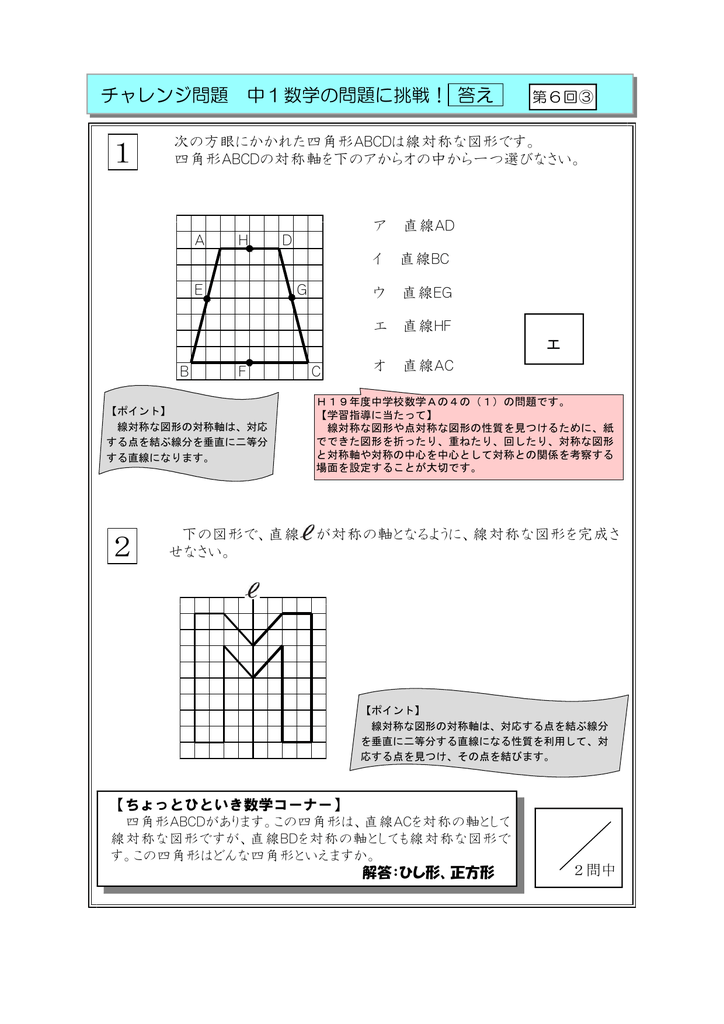



対称軸




世界一分かりやすい算数 小6 対称な図形




世界一分かりやすい算数 小6 対称な図形




6年生のみなさんへ 堀津小blog 羽島市立堀津小学校




世界一分かりやすい算数 小6 対称な図形



成績upストーリー これまで70点台だったのが 入塾後の初テストで満点に 小学6年 幕張西の学習塾 成績upラボ




100点おめでとう 神奈川県相模原市の個別塾 学習塾 ナビ個別指導学院 相模原中央校ブログ




Sqrt2 Lihat Cara Penyelesaian Di Qanda



小学校6年生iさん 身のまわりの図形と対称 の確認テストも100点 学習塾 凛 Rin 静岡県浜松市東区の個人塾
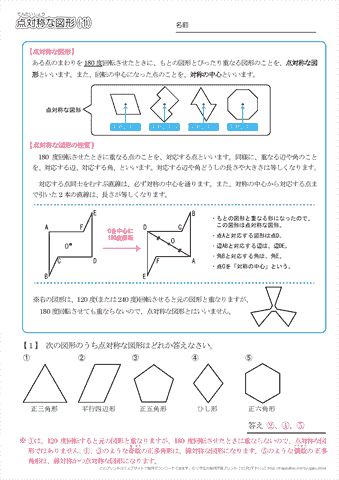



小学6年生の算数 点対称な図形 問題プリント ちびむすドリル 小学生




6年生のみなさんへ 堀津小blog 羽島市立堀津小学校



記事 詳細情報 年 5月 22日 金曜日 6年 6年 算数 対称な図形 週の終わりの金曜日となりました 今週もよくがんばりましたね さて 気付いた人もいるかもしれませんが 5月の算数プリントは授業のノートに雰囲気を近づけています 少しでも



1
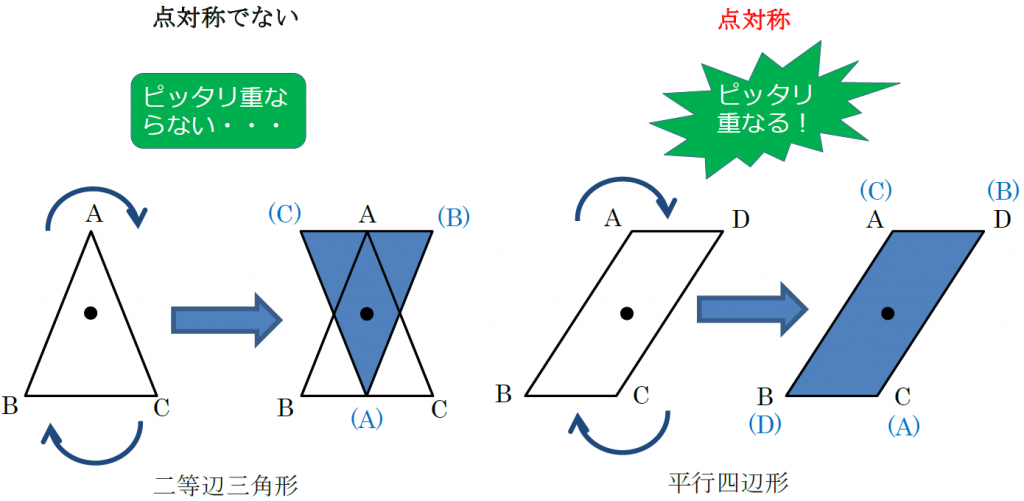



中1数学 点対称な図形とは まなビタミン




世界一分かりやすい算数 小6 対称な図形




世界一分かりやすい算数 小6 対称な図形




対称な図形 線対称と点対称 小学生 算数のノート Clear



貝塚市立南小学校




いろいろ 6 年生 自主学習算数 シモネタ



1




Primary算数的小六の復習 線対称 点対称な図形 筆記 Clear



小学生も点数アップ 岐阜県羽島郡岐南町の個別塾 学習塾 ナビ個別指導学院 岐南町校ブログ



線対称との違いは 点対称 な図形を理解しよう お役立ち情報ページ 個別指導の学習塾なら個別指導塾スタンダード




算数 対称な図形 学校そっくりテスト かなた君満点 コロンビア塾 中学校夏休み31日まで延長



点対称な図形 問題プリント まとめテスト 小学6年生用無料算数プリント
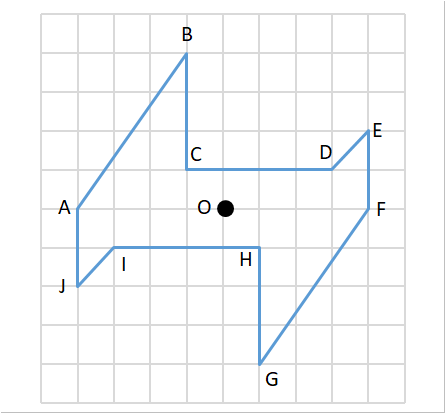



中山先習塾 練習問題 テストが作動しないときは Internet Explorerをお試しくださいワン 小6 B 対称な図形 点対称 対称の軸 対応する点 中心を通り同距離 100 点満点 合格点 設定なし 残り時間 テスト開始 テストを開始するには




ヤフオク 0422g 010 新学習指導要領対応 プレテストつき
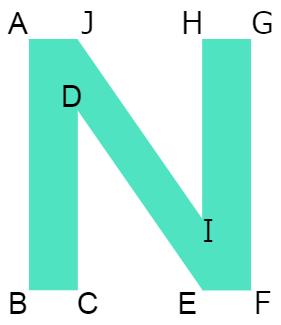



点対称な図形 問題プリント まとめテスト 小学6年生用無料算数プリント ページ 2




線対称 点対称の定義と違い 簡単な見分け方を解説 数学fun
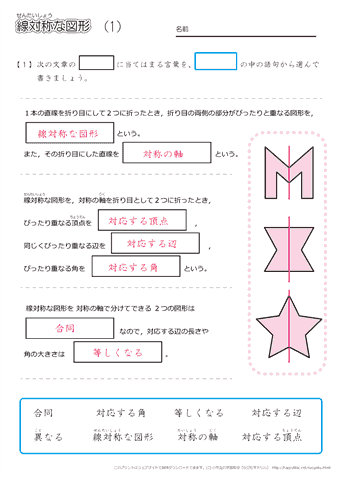



小学6年生の算数 線対称な図形 問題プリント ちびむすドリル 小学生



堺市立西百舌鳥小学校 のホームページ



Http Www Kushiro Ed Jp Kyoei E Htdocs Action Common Download Main Upload Id 3116



記事 詳細情報 年 5月 22日 金曜日 6年 6年 算数 対称な図形 週の終わりの金曜日となりました 今週もよくがんばりましたね さて 気付いた人もいるかもしれませんが 5月の算数プリントは授業のノートに雰囲気を近づけています 少しでも



無料 中1数学 テスト対策問題 問題プリント 125 平面図形1 直線と角 対称



堺市立西百舌鳥小学校 のホームページ
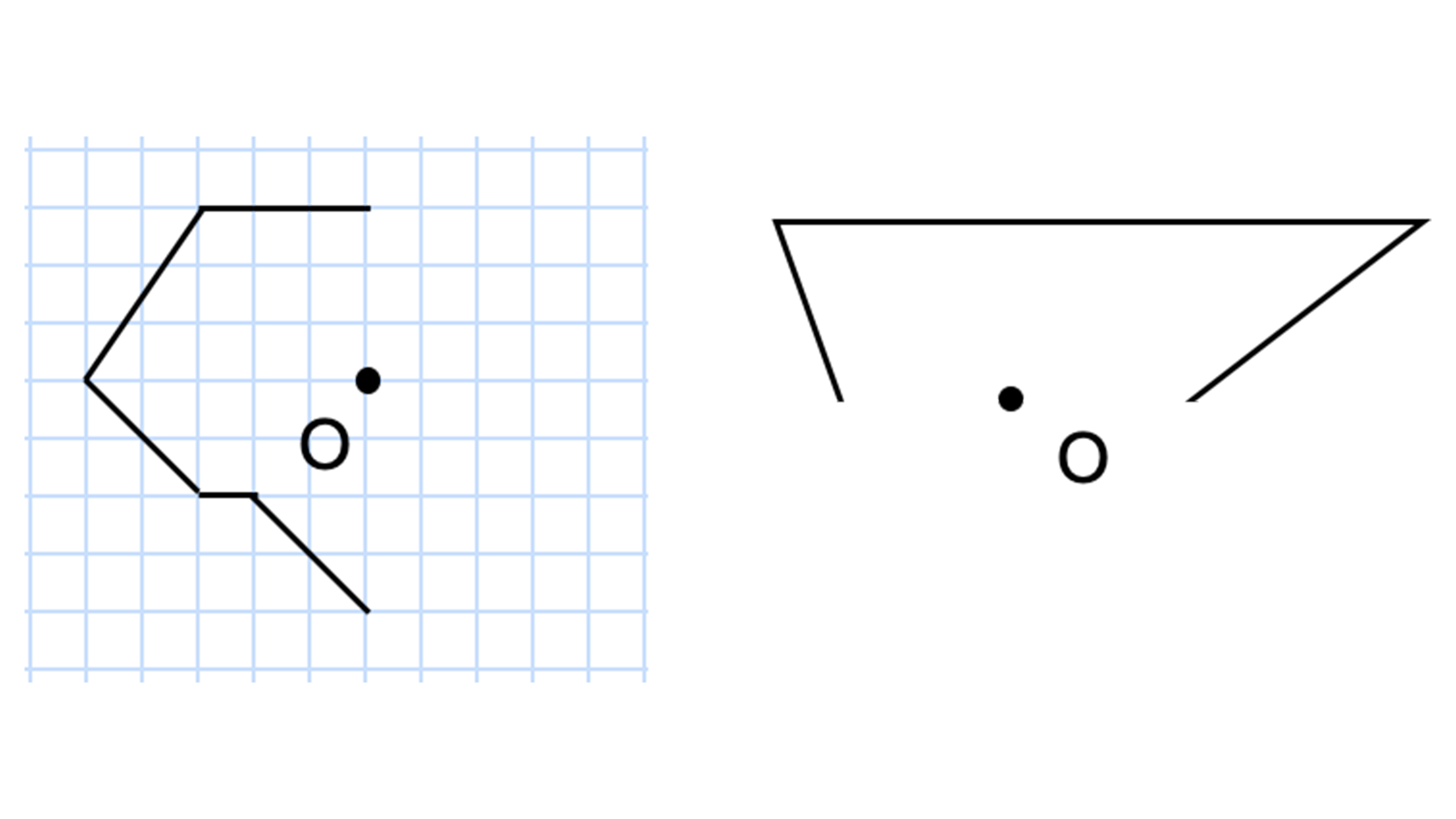



線対称との違いは 点対称 な図形を理解しよう お役立ち情報ページ 個別指導の学習塾なら個別指導塾スタンダード




8 31まで おためし問題集特典つき 天才ドリル 平面図形が得意になる点描写 線対称 小学校全学年用 算数 考える力を育てる 認知工学 本 通販 Amazon


